드래프트 (draft)
2019.07.07문제
드래프트는 스포츠 팀들이 새로운 신인 선수들을 공평하게 영입하기 위해 시행하는 제도이다. 각 팀들은 차례를 정한 후, 돌아가면서 선수들을 지명한다. 하지만, 드래프트에서 많은 팀들이 원하는 선수가 있을 때는 팀들 간에 보이지 않는 수싸움이 이어지기도 한다.
올해의 드래프트는 다음과 같은 방법으로 진행된다고 한다.
- N명의 선수들에게 1, 2, …, N 번호가 부여된다.
- 팀들은 1번 선수부터 차례대로 선수들을 지명한다.
- 먼저 지명하는 팀은 1명의 선수 (1번) 또는 2명의 선수(1, 2번)를 지명할 수 있다.
- 이후에는 전 팀이 지명한 선수 수의 2배 이하만큼 선수를 지명할 수 있다.
올해 드래프트에는 당신과 당신의 라이벌 팀, 2개의 팀이 참여했다. 당신은 유능한 전력분석관이기 때문에, 드래프트에서 영입할 수 있는 선수들의 가치를 전부 알고 있다. 그러나, 상대 팀 또한 호락호락하지 않기 때문에 마찬가지로 선수들의 가치를 잘 알고 있으며, 드래프트에서 가치가 높은 선수들을 데려가기 위해 최선을 다할 것이다. 드래프트에서는 당신의 팀이 먼저 지명을 시작한다.
드래프트에서 어떻게 선수들을 지명해야 당신 팀에서 데려갈 수 있는 선수들의 가치를 최대화할 수 있는지 결정하는 프로그램을 작성하시오.
예시
드래프트의 5명의 선수들이 참여하고, 번호 순서대로 각 선수의 가치가 [1, 3, 1, 7, 2]라고 하자.
이 때, 서로 최선을 다할 경우 다음과 같이 진행된다. (믿지 못하겠으면 직접 다른 방법으로 드래프트를 해 보자.)
| 팀 | 뽑은 선수 |
|---|---|
| 당신의 팀 | 1 |
| 상대 팀 | 3 |
| 당신의 팀 | 1, 7 |
| 상대 팀 | 2 |
따라서 당신의 팀이 데려갈 수 있는 선수들의 가치의 최대값은 9이다.
관찰
이전에 다루었던 게임 문제(베스킨라빈스 31 (br31))와 마찬가지로, 두 명의 플레이어가 규칙 하에 경쟁하는 게임입니다. 이 문제 또한 “베스킨라빈스 31” 문제와 마찬가지로 게임의 상태를 몇 번 선수까지 데려갔는지와 상대가 전 차례에 몇 명의 선수를 데려갔는지로 나타낼 수 있습니다. 다만, “베스킨라빈스 31” 문제와 달리 이 문제에서는 승/패가 결정되는 것이 아니라, 주어진 상황에서 최대한 이득을 보는 문제입니다. 그러나, 이 문제 또한 상태 그래프를 통해 나타내고 이 그래프 상에서 풀이를 생각해 볼 수 있습니다.
상태 그래프를 만들기 위해서 어떤 상태 [n, k] (N명 중 n번 선수까지 데려갔고, 이전 차례에 상대가 k명의 선수를 데려간 상황)에서 이동할 수 있는 상태가 무엇인지 생각해 봅시다. 이번 턴에 우리 팀은 1명의 선수부터 2k명의 선수까지 데려갈 수 있습니다. 따라서, 이동할 수 있는 상태들은 [n+1, 1], ..., [n+2k, 2k] 까지 최대 2k가지가 됩니다. 문제에서 제시한 예시와 같이 N=5인 경우에는 아래와 같은 상태 그래프를 그릴 수 있습니다.
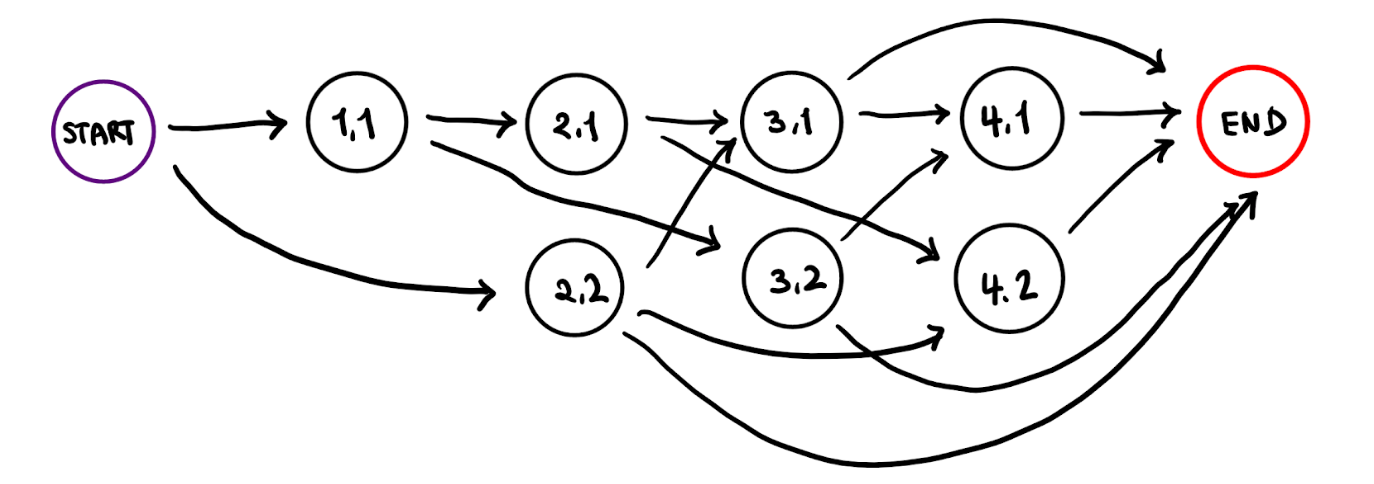
예시와 같이 드래프트가 진행되는 경우,
START -> [1, 1] -> [2, 1] -> [4, 2] -> END
순서대로 상태를 이동하게 됩니다. 상태를 이동하면서 데려간 선수들의 가치를 최대화해야 하는데, 어떻게 할 수 있을까요?
풀이
상태 그래프에서 경쟁하는 상대와의 최적화 - Minimax 알고리즘
이러한 문제에 접근하는 가장 대표적인 알고리즘인 Minimax 알고리즘에 대해 알아봅시다. “베스킨라빈스 31” 문제에서 상태마다 ‘이기는 상태’인지 ‘지는 상태’인지를 표시했던 것과 마찬가지로, 이 문제에서는 각 상태마다 ‘이 상태에서 시작했을 때, 데려갈 수 있는 선수들의 가치의 최대값’을 표시하도록 합시다. (상태 S에 표시한 값을 f(S)라고 표기하겠습니다.) 예를 들어, [4, 1] 상태에서 시작한다면 마지막 5번째 선수만 데려갈 수 있으므로 이 때 상태에 표시할 값은 2가 됩니다. [3, 2] 상태에서 시작한다면 4, 5번째 선수들을 모두 데려갈 수 있으므로, f(3, 2) = 9입니다. 이처럼, 남은 선수들을 모두 데려갈 수 있을 경우에는 남아있는 선수들의 가치의 합이 바로 기록할 값이 됩니다.
하지만, [1, 1]과 같이 이 값을 쉽게 결정할 수 없는 상태의 경우 어떻게 할까요? 다음 상태들에 기록된 값을 보고 결정해야 하는데, 까다로운 점은 상대방이 다음 상태에서 시작하게 된다는 점입니다. 여기에 적용되는 Minimax 알고리즘의 원리는 다음과 같습니다.
제로섬(zero-sum) 게임에서, 상대방이 얻을 수 있는 최대 이득을 최소화하는 방향으로 게임을 진행한다.
제로섬 게임이란 상대방이 얻는 이득이 나의 손해가 될 때, 다시 말해 win-win이 불가능한 게임을 말합니다. 드래프트에서 데려갈 수 있는 선수들은 정해져 있으므로, 어떤 선수를 상대방이 데려가 버리면 그 선수는 우리 팀에서 데려갈 수 없습니다. 따라서, 이 문제에서 다루는 드래프트 게임은 제로섬 게임의 정의에 들어맞습니다. Minmax 알고리즘의 원리에 의해, 상대방의 이득(상대방이 데려가는 선수들의 가치)을 최소화하는 것이 우리의 이득을 최대화하는 것과 동일합니다.
상대방도 마찬가지의 생각으로 드래프트를 진행하기 때문에, 내 차례에 S라는 상태에서 S’라는 상태로 이동하게 된다면, 상대는 S’에서 이동할 상태 중 내가 얻는 이득이 최소인 상태로 이동시킬 것입니다. 따라서, 거꾸로 생각하면 나는 S’를 고를 때 S’에서 이동할 상태 S’’ 중 내가 얻는 이득이 최소인 경우를 최대화해야 합니다. (이 논리 때문에 알고리즘이 Minimax 알고리즘이라고 불립니다.)
정리하면,
\[f(S) = \textrm{max}_{S \rightarrow S'} \{ \textrm{min}_{S' \rightarrow S''} f(S'') + (S \rightarrow S' \textrm{로 갈 때 얻는 이득}) \}\]이해를 돕기 위해 f(2, 1)의 값을 계산해 봅시다. [2, 1]에서 이동할 수 있는 상태는 [3, 1]과 [4, 2]입니다.
S’ = [3, 1]인 경우, 그 다음 상태S’’는[4, 1]과END(모든 선수를 뽑은 경우)가 가능합니다.f(4, 1) = 2이고f(END) = 0이기 때문에,min f(S’’) = 0입니다.S’ = [4, 2]인 경우, 마찬가지로 다음 상태는END이기 때문에min f(S’’) = 0입니다.
두 경우에서 min f(S’’) + (S -> S’로 갈 때 얻는 이득)을 계산하면,
S’ = [3, 1]로 이동할 때는0 + (1) = 1S’ = [4, 2]로 이동할 때는0 + (1 + 7) = 8
따라서 f(2, 1) = 8입니다. 실제로, 가치가 각각 1, 7, 2인 선수 3명이 남아 있고 처음에 2명까지 데려갈 수 있는 경우를 생각해 보면, 당연히 처음 데려가는 팀이 1, 7 두 명을 데려가는 것이 최선이라는 것을 알 수 있습니다.
마찬가지로, f(START)의 값을 계산해 봅시다.
S’ = [1, 1]: min( f(2, 1), f(3, 2) ) + 1 = min( 8, 9 ) + 1 = 9S’ = [2, 2]: min( f(3, 1), f(4, 2), f(END) ) + (1 + 3) = min( 9, 2, 0 ) + 4 = 4
따라서 f(START) = 9가 되며, S’ = [1, 1]로 이동하는 것이 최적이므로 처음에 선수 1명을 뽑아야 한다는 것도 알 수 있습니다!
어떤 상태 [n, k]에서 다음 상태 [n+i, i]로 이동할 때 얻는 이득은 n+1번째 선수부터 n+i번째 선수들의 가치의 합입니다. 이 합은 직접 선수들의 가치를 일일이 더해 구할 수도 있고 (시간복잡도 \(O(N)\)), 미리 계산한 누적 합 배열을 통해 빠르게 \(O(1)\)에 계산할 수도 있습니다.
다음은 Minimax 알고리즘을 바탕으로 생각한 풀이의 의사코드입니다.
# values: 선수들의 가치 리스트.
def solution(N, values):
# 전처리: 누적 합 배열을 계산한다.
s = [0] * N
for i in range(N):
s[i] = s[i-1] + values[i] if i > 0 else values[i]
# f[n][k] = 상태 [n, k]에서 시작했을 때 얻을 수 있는 최대 이득
f = [[0] * (N+1)] * N
for n in N-1 ... 0: # 뒤쪽 상태부터 거꾸로 계산한다.
for k in 1 ... N:
if n + 2*k >= N: # 남은 선수를 모두 데려갈 수 있을 경우
f[n][k] = s[N] - s[n]
else
f[n][k] = max(
min(f[n+1+1][1], ..., f[n+1+2][2]) + s[n+1] - s[n],
min(f[n+2+1][1], ..., f[n+2+4][4]) + s[n+1] - s[n],
...,
min(f[n+k+1][1], ..., f[n+k+2*k][2*k]) + s[n+k] - s[n]
)
# 맨 처음 상태는 [0, 1]이다. (다음 상태가 [1, 1], [2, 2]이므로)
return f[0][1]
이 의사 코드의 시간 복잡도는 어떻게 될까요? 2중 for 루프를 통해 [n, k] 상태를 전부 고려해야 하고, 각 상태마다 max, min을 계산해야 합니다. 따라서, 이처럼 단순히 식을 따라 계산했을 때는 식을 계산하는 데 \(O(N^2)\)의 시간 복잡도가 필요하고, 전체적으로는 \(O(N^4)\)의 시간 복잡도가 필요합니다.
수식의 특징을 통해 시간 복잡도 줄이기
\(O(N^4)\) 시간 복잡도는 제로섬 게임의 Minimax 알고리즘의 원리로부터 도출한 식을 그대로 적용했을 때 얻을 수 있는 시간 복잡도입니다. 이 식을 그대로 계산하지 말고, 문제의 특징을 고려하여 더 빠르게 계산할 수 있는 방법을 생각해 봅시다.
위에서 다뤘던 식
\[f(S) = \textrm{max}_{S \rightarrow S'} \{ \textrm{min}_{S' \rightarrow S''} f(S'') + (S \rightarrow S' \textrm{로 갈 때 얻는 이득}) \}\]을 누적 합 배열 S[]를 이용하여 다시 적으면 다음과 같습니다.
\[f(n, k) = \textrm{max}_{i=1,\cdots,2k} \{ \textrm{min}_{j=1,\cdots,2i} f(n+i+j,j) + (S[n+i] - S[n]) \}\]여기에서 max와 관계 없는 S[n]을 바깥으로 빼면,
\[f(n, k) = \textrm{max}_{i=1,\cdots,2k} \{ \textrm{min}_{j=1,\cdots,2i} f(n+i+j,j) + S[n+i] \} - S[n]\]이 식에서 \(\textrm{max}\) 안에 있는 부분인 \(\textrm{min} f(n+i+j, j) + S[n+i]\)를 보면, 바깥쪽의 형태인 \(\textrm{max}\{ \cdot \} - S[n]\)과 상당히 유사함을 알 수 있습니다. 따라서
\[g(n, k) = \textrm{min}_{i=1,\cdots,2k} f(n+i, i) + S[n]\]이라고 정의하면, 다음과 같은 관계를 얻을 수 있습니다.
\[f(n, k) = \textrm{max}_{i=1,\cdots,2k} g(n+i, i) - S[n]\]식의 유사성을 활용하여, f(n, k)와 g(n, k)를 둘 다 계산해 나가면 원래 식에서 \(\textrm{max}\{\textrm{min} \{\cdot\}\}\) 을 계산하는 데 필요한 \(O(N^2)\) 시간 복잡도를 \(O(N)\)으로 줄일 수 있습니다. 따라서, 전체 시간 복잡도는 \(O(N^4)\)에서 \(O(N^3)\)으로 줄일 수 있습니다.
더 효율적으로 계산할 수 있을까요? 예를 들어, f(n, k)와 f(n, k+1)을 계산하는 과정에서 살펴보아야 하는 g(n+i, i)들을 나열해 보면 다음과 같습니다.
f(n, k) : g(n+1, 1), ..., g(n+2k, 2k)
f(n, k+1) : g(n+1, 1), ..., g(n+2k, 2k), g(n+2k+1, 2k+1), g(n+2k+2, 2k+2)
f(n, k+1)를 계산하는 과정에서 이미 f(n, k)를 계산할 때 고려했던 g(n+i, i) 값들을 다시 살펴보고 있다는 것을 알 수 있습니다. 중복되는 계산을 없애면 다음과 같이 쓸 수 있겠네요.
f(n, k+1) = max{ f(n, k), g(n+2k+1, 2k+1) - S[n], g(n+2k+2, 2k+2) - S[n] }
마찬가지로,
g(n, k+1) = min{ g(n, k), f(n+2k+1, 2k+1) + S[n], f(n+2k+2, 2k+2) + S[n] }
이처럼 계산하면 각 f(n, k)를 계산할 때 2k개의 g(n+i, i)를 보는 것이 아니라, 이전 f(n, k-1)값을 활용하여 최대 2개만 살펴보게 되므로 식을 계산하는 데 필요한 시간 복잡도가 \(O(1)\)로 줄어듭니다. 따라서, 최종적으로 전체 시간 복잡도를 \(O(N^2)\)까지 줄일 수 있습니다.
# values: 선수들의 가치 리스트.
def solution(N, values):
# 전처리: 누적 합 배열을 계산한다.
s = [0] * N
for i in range(N):
s[i] = s[i-1] + values[i] if i > 0 else values[i]
# f[n][k] = 상태 [n, k]에서 시작했을 때 얻을 수 있는 최대 이득
f = [[0] * (N+1)] * N
g = [[0] * (N+1)] * N
for n in N-1 ... 0: # 뒤쪽 상태부터 거꾸로 계산한다.
for k in 1 ... N:
if n + 2*k >= N: # 남은 선수를 모두 데려갈 수 있을 경우
f[n][k] = s[N] - s[n]
g[n][k] = s[n]
else # 최적화한 식을 사용한다.
f[n][k] = max(f[n][k-1], max(g[n+2*k+1][2*k+1], g[n+2*k][2*k]) - s[n]
g[n][k] = min(g[n][k-1], min(f[n+2*k+1][2*k+1], f[n+2*k][2*k]) + s[n]
# 맨 처음 상태는 [0, 1]이다. (다음 상태가 [1, 1], [2, 2]이므로)
return f[0][1]
입력/출력 예제
입력 형식
- 첫 번째 줄에는 드래프트에 나온 선수의 수 N이 주어진다. (1 <= N <= 2,000)
- 다음 N개의 줄에는 각 선수의 가치 p_i가 주어진다. (1 <= p_i <= 100,000)
출력 형식
- 당신이 이 드래프트에서 영입할 수 있는 선수들의 가치 합의 최대값을 출력한다.
입력 예제 1
5
1
3
1
7
2
출력 예제 1
9
원문
Farmer John’s cows like to play coin games so FJ has invented with a new two-player coin game called Xoinc for them.
Initially a stack of N (5 <= N <= 2,000) coins sits on the ground; coin i from the top has integer value C_i (1 <= C_i <= 100,000).
The first player starts the game by taking the top one or two coins (C_1 and maybe C_2) from the stack. If the first player takes just the top coin, the second player may take the following one or two coins in the next turn. If the first player takes two coins then the second player may take the top one, two, three or four coins from the stack. In each turn, the current player must take at least one coin and at most two times the amount of coins last taken by the opposing player. The game is over when there are no more coins to take.
Afterwards, they can use the value of the coins they have taken from the stack to buy treats from FJ, so naturally, their purpose in the game is to maximize the total value of the coins they take. Assuming the second player plays optimally to maximize his own winnings, what is the highest total value that the first player can have when the game is over?
출처
USA Computing Olympiad, 2009 November Contest, Silver, Problem 1 (xoinc)