베스킨라빈스 31 (br31)
2019.05.22문제
“베스킨라빈스 31”은 아주 유서 깊고 오래된 게임으로, 다음과 같은 규칙으로 진행된다.
- 1부터 시작하여 한 명씩 차례대로 숫자를 부른다. 각 사람은 1개부터 3개까지의 숫자를 부를 수 있다.
- 31을 부르는 사람이 패배한다.
이 게임은 많은 사람들이 있을 때 하면 결과를 예측할 수 없어 스릴이 넘치지만, 만약 두 명이 이 게임을 한다면 반드시 시작하는 사람(선공)이 이기게 되므로 재미가 없다. 따라서 “업그레이드”라는 규칙을 추가했다.
- 업그레이드: 바로 전 사람이 부른 숫자의 개수만큼 숫자를 부르면 패배하게 된다. 예를 들어, 이전 사람이 2개의 숫자를 불렀다면 다시 2개의 숫자를 부를 수 없다.
“베스킨라빈스 N” 게임을 진행할 때, 선공과 후공 중 누가 이기게 되는지 예측하는 프로그램을 작성하시오.
예시
N = 1인 경우, “베스킨라빈스 1” 게임에서는 시작하는 사람이 1을 부르는 순간 패배하므로 후공이 승리한다.N = 3인 경우, “베스킨라빈스 3” 게임에서는 선공이 1, 2를 부르면 무조건 승리할 수 있다.
관찰
아마 기존의 “베스킨라빈스 31” 게임을 이미 알고 있었던 사람이라면, 두 명이 이 게임을 할 때 (N > 1인 경우에) 어떻게 선공이 게임을 진행해야 무조건 승리할 수 있는지도 알고 있을 것입니다.
- 31을 부르면 게임을 지게 되므로, 게임을 이기려면 30을 불러 상대방이 31을 부를 수밖에 없게 만들어야 합니다.
- 30을 부르려면, 26을 불러야 합니다. 26을 부른 경우 상대방이 어떻게 숫자를 불러도 무조건 30을 부를 수 있습니다.
- 이 과정을 반복하면,
30 -> 26 -> 22 -> ... -> 6 -> 2순으로 부르면 이기는 숫자가 결정되므로 첫 사람이1, 22개의 숫자를 부르면 승리한다는 사실을 알 수 있습니다.
일반적으로, 업그레이드 규칙이 추가되지 않은 “베스킨라빈스 N” 게임에서, 1, 2, …, M개의 숫자를 부를 수 있을 경우, N-1을 부르면 승리하므로 선공이 (N-1) % (M+1) 개의 숫자를 부르는 것으로 시작하면 무조건 승리합니다. 만약 (N-1) % (M+1) = 0인 경우 후공이 승리하게 됩니다. 따라서, N과 M이 주어졌을 때 선공과 후공 중 누가 승리하는지를 \(O(1)\) 상수 시간 복잡도로 바로 결정할 수 있습니다.
하지만, 업그레이드 규칙이 추가된 경우 얘기가 달라집니다. 예를 들어, 선공이 게임을 잘 진행하여 26까지 불렀는데, 기존의 규칙에서는 후공이 27, 28을 부른 경우 선공이 29, 30을 불러 승리할 수 있었지만 업그레이드 규칙에 의해 29, 30을 부를 수 없게 됩니다. 그렇다면 어떻게 생각해야 업그레이드 규칙에서 게임의 결과를 예측할 수 있을까요?
풀이
상태 그래프
어떤 베스킨라빈스 31 게임에서, 게임이 다음과 같이 진행되었다고 생각해 봅시다.
- 선공: 1, 2
- 후공: 3
- 선공: 4, 5, 6
- 후공: 7, 8
다른 게임에서는, 이렇게 진행되었다고 합시다.
- 선공: 1, 2, 3
- 후공: 4, 5
- 선공: 6,
- 후공: 7, 8
두 게임의 진행 과정은 분명 다르지만, 마지막 사람이 7, 8 두 개의 숫자를 불렀다는 점이 공통점입니다. 이 때, 두 게임의 상태는 정확히 동일합니다. 즉, 게임의 과거 진행 과정에 상관 없이 마지막 숫자와 마지막 사람이 부른 숫자의 개수만으로 게임의 상태를 표현할 수 있습니다.
“베스킨라빈스 5” 게임에서 3개의 숫자까지 부를 수 있을 때, 이 게임을 9개의 일반 상태와 시작 상태, 패배한 상태(5를 불러야 할 때)까지 총 11개의 상태로 나타낼 수 있습니다. 그림으로 나타내면 다음과 같습니다.
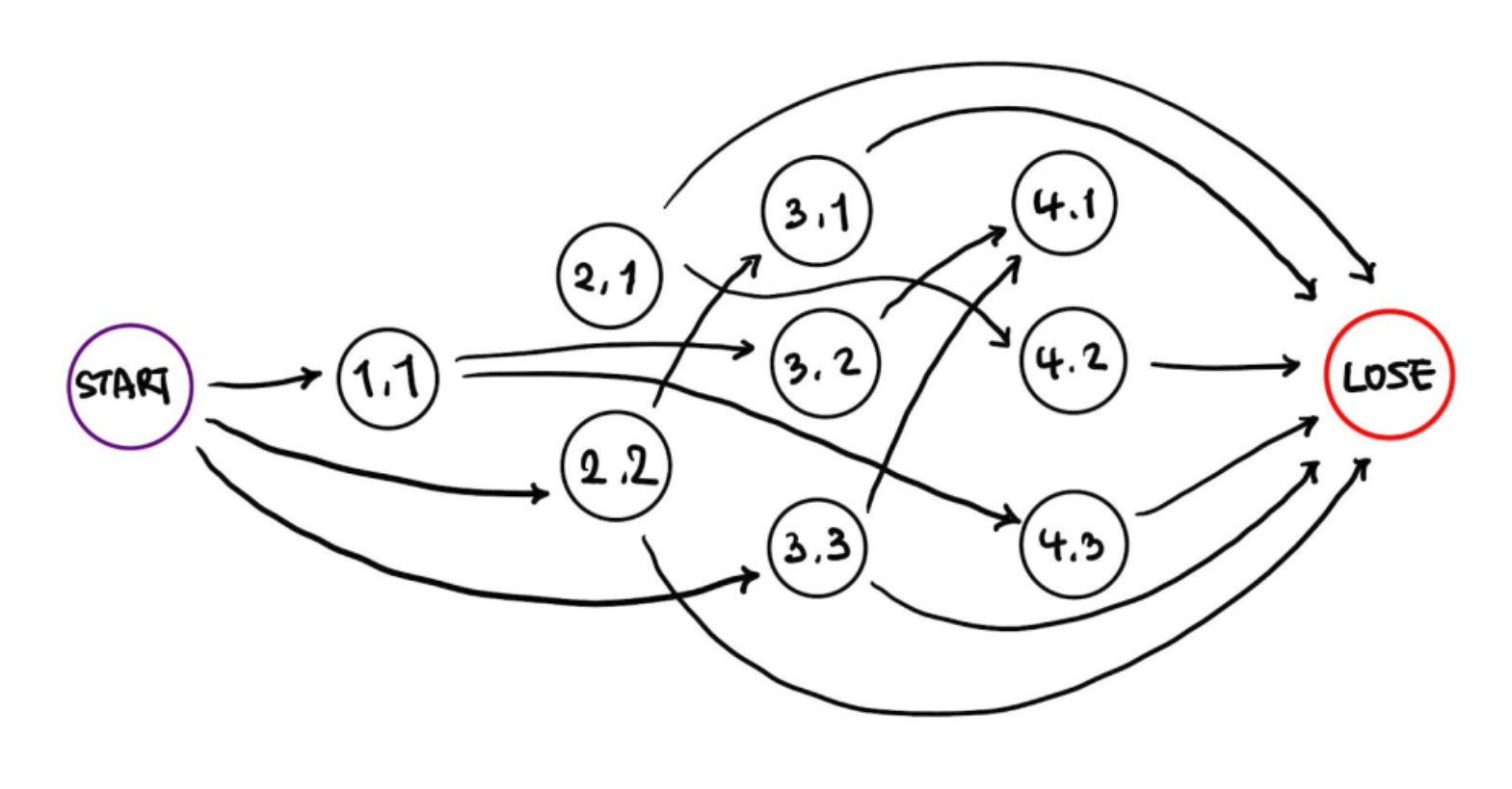
각 화살표는 어떤 상태에서 이동할 수 있는 다음 상태로의 경로를 나타냅니다. 예를 들어, 다음과 같이 진행된 게임을 생각해 봅시다.
- 선공: 1, 2
- 후공: 3
- 선공: 4, 5 (패배)
이 게임은 위 그림에서 다음과 같은 경로로 나타낼 수 있습니다.
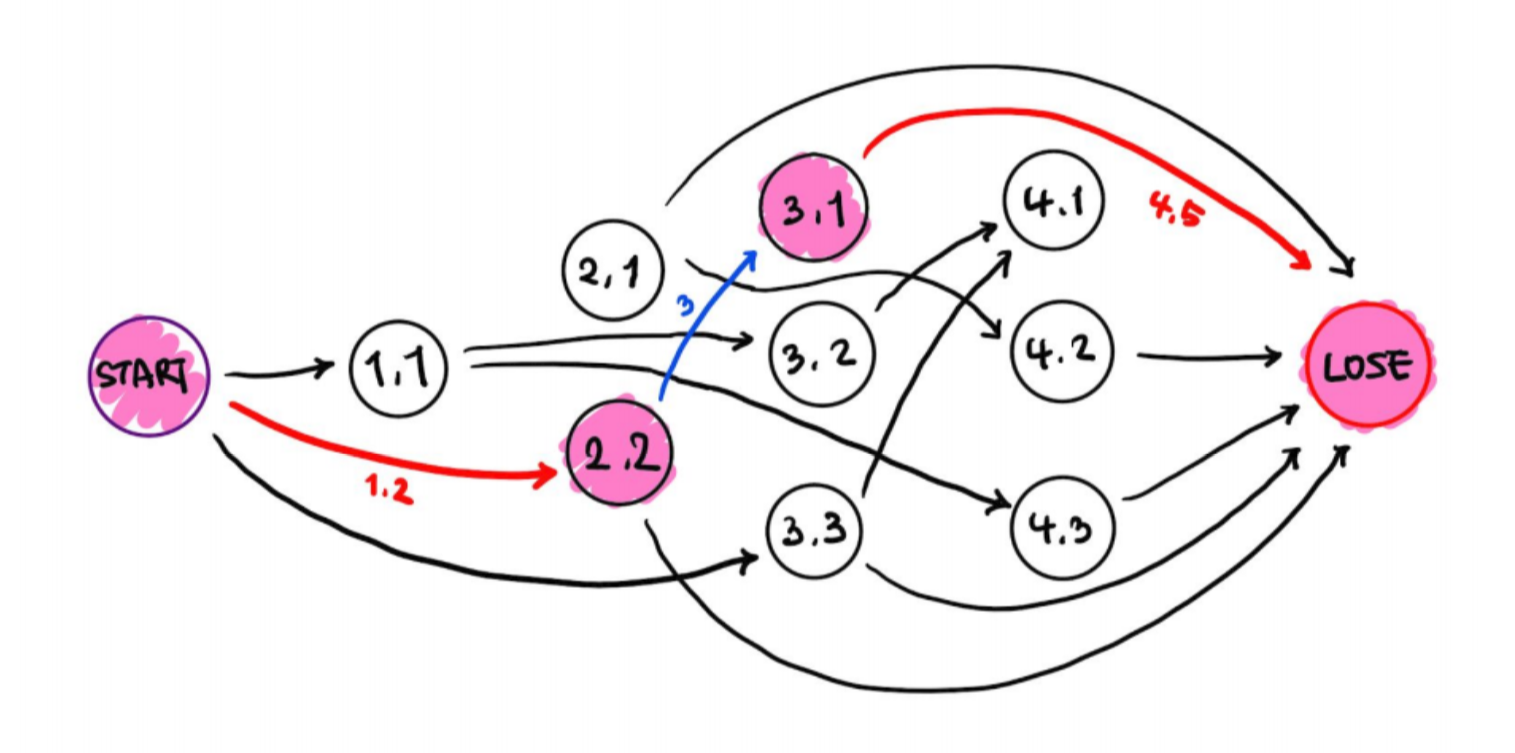
일반적으로, (n, k)라는 상태(마지막으로 부른 숫자가 n이고, 마지막 사람이 부른 숫자의 개수가 k개일 때)에서 연결할 수 있는 상태들은 (n+1, 1), (n+2, 2), ... , (n+k-1, k-1), (n+k+1, k+1), ..., (n+M, M) 까지 최대 M-1 가지가 됩니다.
상태 그래프에서 승패 예측하기
게임의 상태를 서로 연결한 그래프를 만든 후, 이 그래프에서 베스킨라빈스 게임의 승패를 어떻게 예측할 수 있는지 생각해 봅시다.
어떤 상태에서 이동할 수 있는 상태가 LOSE 뿐인 경우, 무조건 패배하게 됩니다. 예를 들어 앞에서 본 예시와 같이, “베스킨 라빈스 5” 게임에서 (3, 1) 상태, 즉 상대방이 3을 부른 경우 다음 차례에서 4, 5를 부를 수밖에 없기 때문에 패배하게 됩니다. 또한, 이동할 수 있는 상태가 없는 경우(업그레이드 규칙을 어길 수 밖에 없는 경우)도 패배하는 상태입니다. 그래프에서 패배하는 상태를 색칠하도록 하겠습니다.
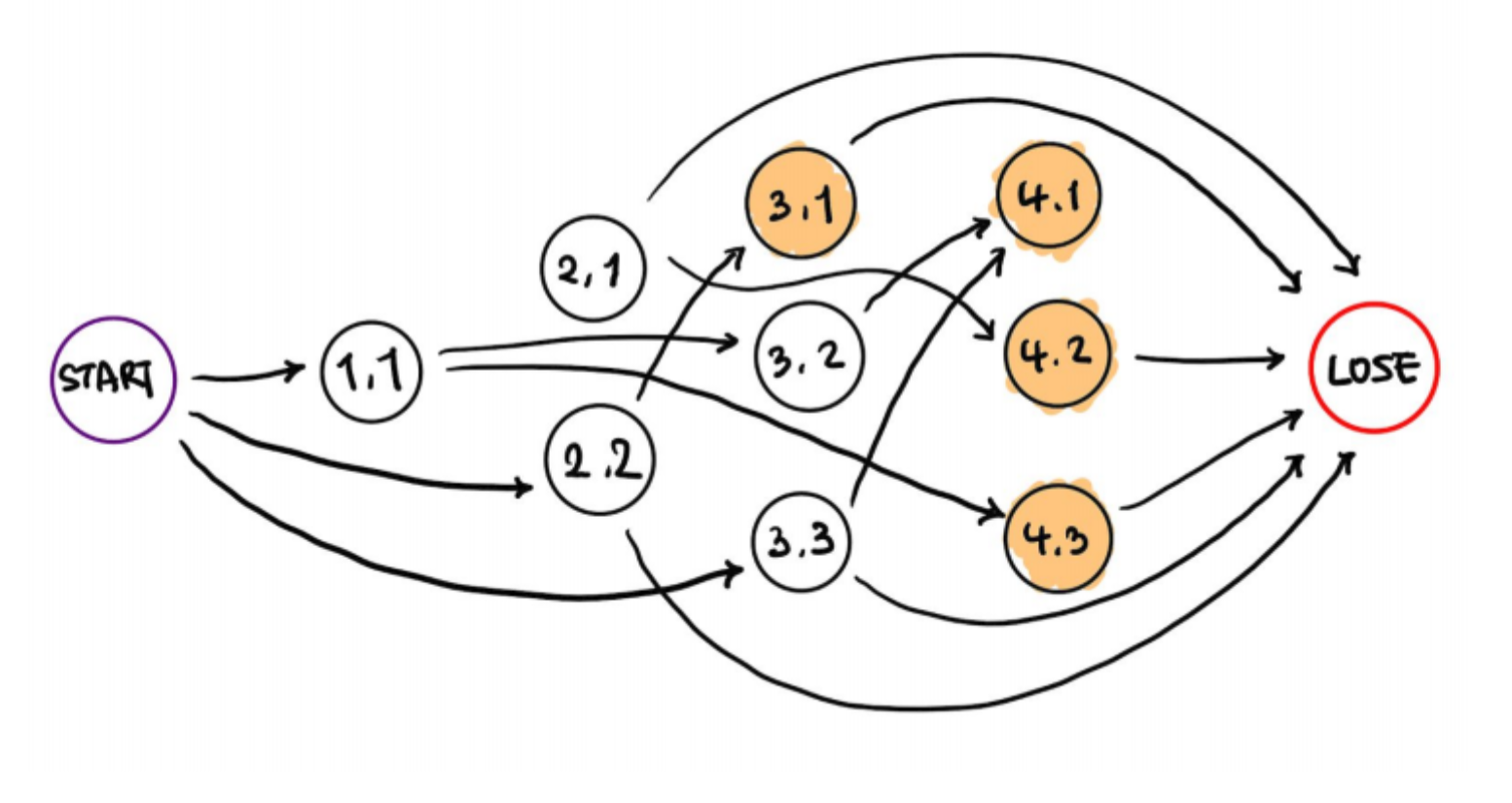
여기에서 (4, k)와 같은 상태는 모두 색칠되어 있는데, 이는 이미 우리가 알고 있는 사실인, 4를 상대방이 부르면 무조건 패배한다는 것과 함께 해석할 수 있습니다.
이제 만약 우리에게 (1, 1)과 같은 상태(즉, 상대가 ‘1’을 부른 후 우리 차례일 때)가 주어졌다고 생각해 봅시다. (1, 1)은 (3, 2)와 (4, 3)으로의 경로를 가지고 있습니다. 그런데, (4, 3)은 무조건 패배하는 상태이므로, 우리가 (1, 1)에서 (4, 3)으로의 경로를 선택할 경우 상대방은 (4, 3) 상태에서 패배하게 됩니다. 일반적으로 생각하면, 어떤 상태에서 패배하는 상태로 가는 경로가 존재할 경우, 그 상태는 승리하는 상태가 됩니다. 승리하는 상태도 그래프에 색칠해 보겠습니다.
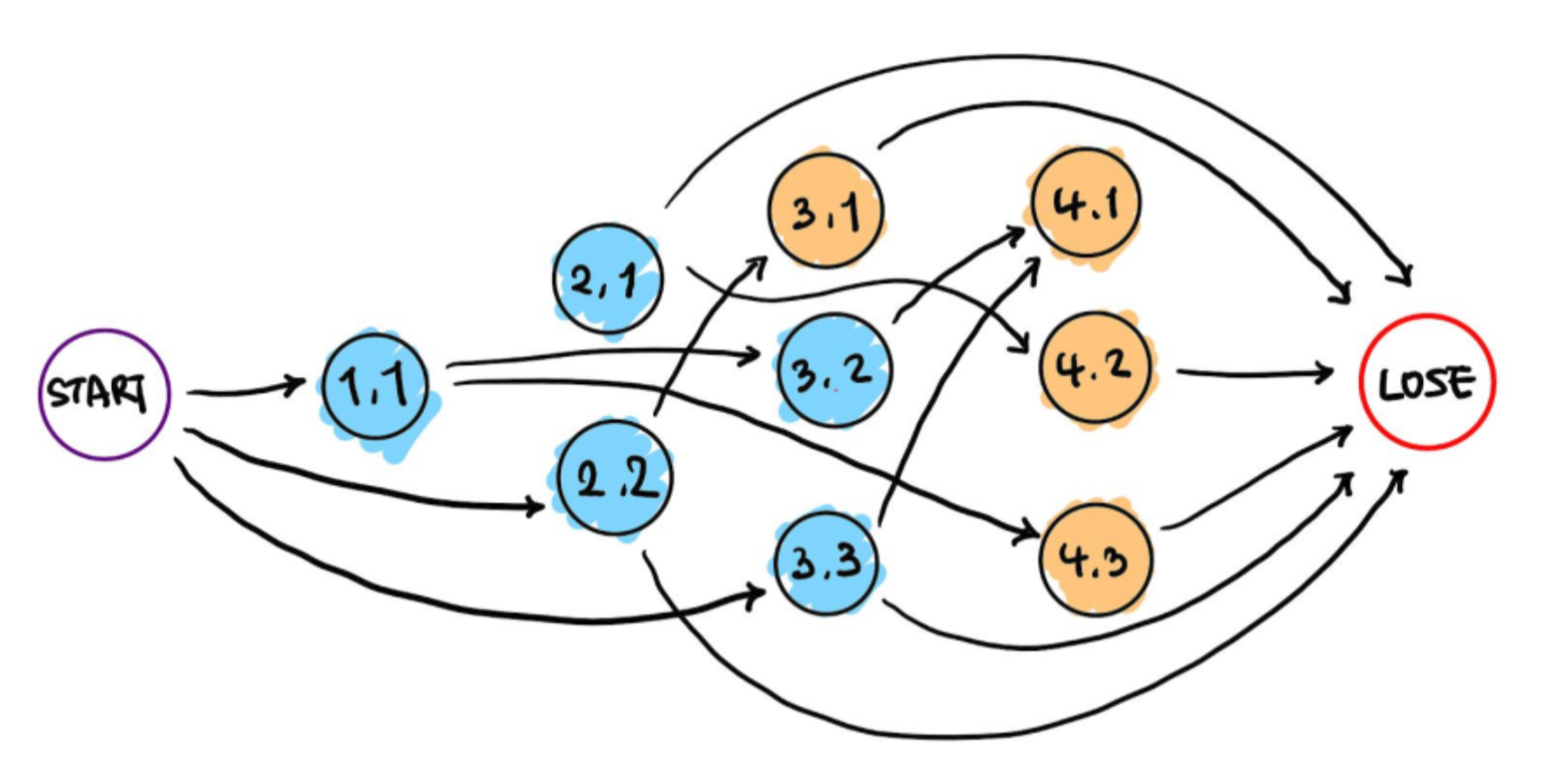
마지막으로, START와 같이 패배하는 상태로 가는 경로가 존재하지 않는 경우를 생각해 봅시다. 이 경우, 어떤 경로를 선택하더라도 상대에게 승리하는 상태를 쥐어줄 수밖에 없습니다. 따라서, 어떤 상태에서 모든 경로가 승리하는 상태로 이어지는 경우, 그 상태는 패배하는 상태가 됩니다.
지금까지 알아낸 규칙을 정리하면,
- 처음에 패배하는 상태를 결정한다. (이동할 수 있는 상태가
LOSE뿐이거나 없는 경우) - 어떤 상태에서,
- 패배하는 상태로의 경로가 존재할 경우, 그 상태는 승리하는 상태이다.
- 패배하는 상태로의 경로가 존재하지 않을 경우, 그 상태는 패배하는 상태이다.
위의 예시의 경우 START가 패배하는 상태이므로, 선공이 무조건 패배한다는 사실을 알 수 있습니다. 직접 후공으로 플레이하면서, 선공이 어떻게 게임을 시작해도 그래프에서 경로를 따라가며 이길 수 있다는 점을 이해해 보시기 바랍니다.
시간 복잡도 분석
“베스킨 라빈스 N” 게임에서 최대 M개의 숫자를 부를 수 있을 때, 방금 소개한 알고리즘의 시간 복잡도를 분석해 보도록 합시다. 이 게임에는 대충 NM개의 상태가 존재합니다. 어떤 상태의 승리, 패배 여부를 결정하기 위해서는 다음 상태 M-1개를 보고 결정해야 하므로, 최종적인 시간 복잡도는 \(O(NM^2)\)입니다.
입력/출력 예제
입력 형식
게임의 정보 N과 M이 주어진다. 이는 “베스킨 라빈스 N” 게임에서 최대 M개의 숫자를 부를 수 있음을 의미한다.
츨력 형식
선공이 승리하는 경우 0, 후공이 승리하는 경우 1을 출력한다.
입력 예제 1
5 3
출력 예제 1
1