전깃줄 II (wire)

이전 글: 전깃줄 I

전깃줄 I 문제에서 제시한 재귀함수 풀이는 글로 읽었을 때는 그럴듯해 보이지만, 실제로 구현해 보면 풀이에서 제시한 시간복잡도 O(N2)보다 더 오랜 시간이 소요됩니다. 이 글에서는 재귀함수 구현의 문제점을 알아보고 풀이를 개선할 수 있는 방법에 대해 다룹니다.

재귀함수와 캐쉬

전깃줄 문제에서 해답을 구하는 재귀함수 maxL(n)을 구하는 점화식은 다음과 같습니다.

maxL(n) = max( maxL(i) | i < n and b[i] < b[n] ) + 1

점화식을 보면, maxL(n)은 maxL(1), ..., maxL(n-1)의 값을 요구할 수 있습니다. 따라서 maxL(n)을 계산하는 데는 \(O(n)\)의 시간 복잡도가 필요하고, 따라서 해답 f(n) = N - max( maxL(1), ..., maxL(N) )을 구하기 위해서는 \(O(N^2)\) 시간 복잡도가 필요할까요?

실제로는 그렇지 않습니다. 재귀함수가 호출되는 과정을 그림으로 그려 보면 이 점화식의 문제점을 잘 이해할 수 있습니다.

# b = [ ... ]

def maxL(n):
    m = 0
    for i in range(1, n):
        if b[i - 1] < b[n - 1]:             # 리스트 인덱스 시작점 맞추기 (-1)
            m = max(m, maxL(i))
    return m + 1

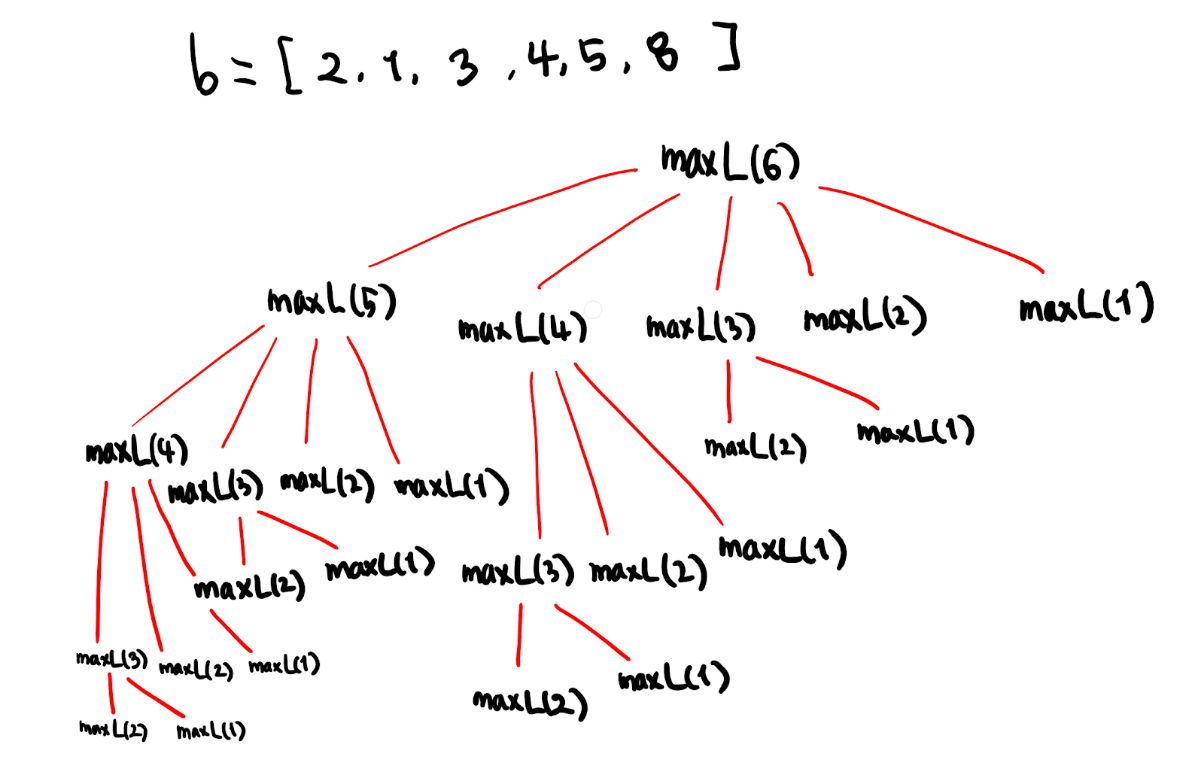
상당히 거대한 탐색 과정입니다. 호출 과정이 복잡해 보이는 이유는 곳곳에 중복된 호출이 포함되어 있기 때문입니다. 예를 들어, maxL(3)을 보면 위 그림에서 총 4번 등장하므로 maxL(6)을 계산하는 과정에서 maxL(3) 함수를 4번 계산하게 됨을 알 수 있습니다. 그러나, 4번 계산해도 maxL(3)의 값은 항상 똑같으므로 이러한 중복 계산은 무의미합니다. 마찬가지로, 그림에서 2번 등장하는 maxL(4)도 두 번 계산할 필요 없이 한 번만 계산하면 됩니다.

이처럼, 재귀함수의 점화식이 자기 자신을 2번 이상 호출하게 되는 경우, 대부분 중복 계산 문제점에 도달하게 됩니다. 특별한 조치를 취하지 않으면 탐색 과정이 아래로 내려갈수록 기하급수적으로 늘어나기 때문에, 우리가 기대하는 \(O(N^2)\) 시간 복잡도가 아니라 \(O(2^N)\), \(O(N^N)\) 등 지수 시간 복잡도를 가지는 알고리즘이 됩니다.

이 문제점에 대한 해법은 간단합니다. 중복 계산을 없애기 위해, 이미 한 번 계산한 적이 있는 함수라면 다시 점화식을 통해 계산하는 것이 아니라 이미 계산한 값을 가져다 쓰는 것입니다. 이처럼 이미 계산한 값을 저장해 두었다가 나중에 필요할 때 재활용하는 것을 캐쉬(cache)라고 부릅니다. 알고리즘 분야에서는 메모이제이션(memoization)이라고 부르기도 합니다.

캐쉬를 활용한 의사코드를 다시 작성해 보고, 재귀함수의 호출 과정을 다시 그림으로 나타내 보겠습니다.

# b = [ ... ]
cache = {}   # 캐쉬 (n을 maxL(n) 값으로 대응시키는 dictionary)
def maxL(n):
    # 캐쉬에 결과가 이미 존재하면, 그 값을 사용한다.
    if n in cache:
        return cache[n]

    # 그렇지 않을 경우, 직접 계산하고 결과를 캐쉬에 저장한다.
    m = 0
    for i in range(1, n):
        if b[i - 1] < b[n - 1]:             # 리스트 인덱스 시작점 맞추기 (-1)
            m = max(m, maxL(i))
    cache[n] = m + 1
    return m + 1

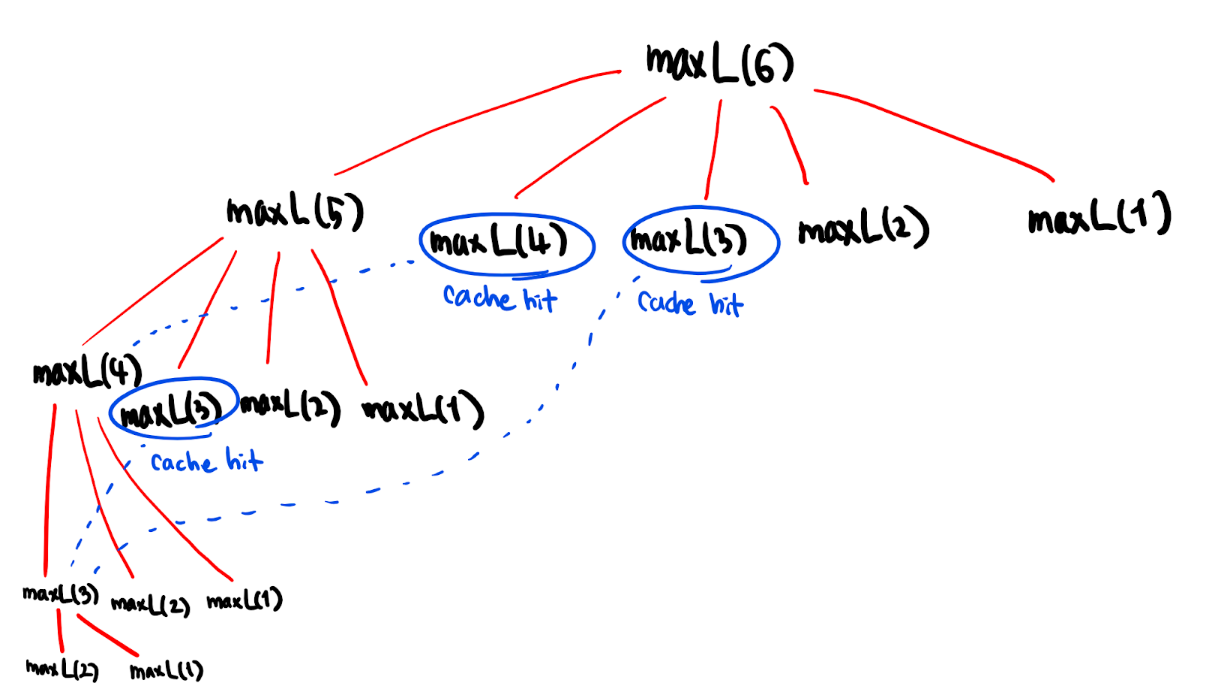
중복 연산이 줄어들면서 탐색 횟수가 많이 감소한 것을 확인할 수 있습니다. 탐색 과정에서 처음 maxL(4), maxL(3)를 만나게 되면, 캐쉬에 값이 존재하지 않으므로 (이러한 상황을 캐쉬 미스 cache miss 라고 부릅니다) 아래쪽의 maxL(2), maxL(1) 등을 더 호출하면서 값을 계산합니다. 이렇게 해서 값을 캐쉬에 집어넣으면, 이후 탐색 과정에서 다시 maxL(4), maxL(3)을 만나게 되었을 때 캐쉬에 값이 존재하는 것을 확인한 후 그 값을 사용(이 상황은 캐쉬 히트 cache hit 라고 부릅니다)하게 됩니다.

캐쉬는 컴퓨터과학에서 광범위한 곳에 활용됩니다. 비교적 적은 양의 메모리를 희생해서 알고리즘의 실행 시간을 대폭 줄일 수 있는 방법이기 때문에 활용법을 잘 알아두는 것이 중요합니다.

캐쉬를 활용하게 되는 경우, 시간 복잡도 분석은 더 어려워집니다. 캐쉬 또한 자료구조이기 때문에, 우리가 원하는 연산(n값에 대응하는 maxL(n) 값을 찾거나 추가하는 연산)을 빠르게 수행하는 자료구조를 사용하는 것이 도움이 됩니다.

심화: python에서 캐쉬 풀이의 시간 복잡도 분석하기

위 python 코드에서 사용한 자료구조는 python dictionary입니다. 캐쉬에 저장하는 ( n, maxL(n) ) 값들은 총 ( 1, maxL(1) )부터 ( N, maxL(N) )까지 최대 N개가 있을 수 있습니다.

Python dictionary에서 어떤 key에 대응하는 value를 찾거나, 새로운 (key, value) 기록을 추가하는 것은 모두 \(O(log N)\) 시간 복잡도가 필요합니다.

maxL(1) 값은 maxL(2), ..., maxL(N)을 호출하면서 최대 N-1번 참조될 수 있습니다. 마찬가지로, maxL(2)는 최대 N-2번, …, maxL(N-1)은 최대 1번 참조됩니다. 캐쉬 참조는 \(O(N^2)\)번 이루어지므로, 캐쉬 참조에 필요한 시간 복잡도는 \(O(N^2 log N)\)이 됩니다.

Python dictionary 말고 python list를 캐쉬 자료구조로 사용하면, 탐색과 기록 추가 모두 \(O(1)\)의 시간 복잡도로 수행할 수 있으므로 전체적인 시간 복잡도가 \(O(N^2)\)로 빨라집니다. 하지만 list를 캐쉬로 사용하면 구현 상에서 여러 가지 처리해주어야 할 점이 있기 때문에 본문의 예제 코드에서는 dictionary를 사용했습니다.

C 언어를 사용할 경우 일반적으로 배열을 통해 캐쉬를 구현하게 됩니다. key가 정수가 아니라서 직접 배열을 사용할 수 없다면 std::map을 사용하거나, key에 해쉬 함수를 적용하여 정수로 간접적으로 바꾸는 방법을 사용합니다.

재귀함수와 반복문

재귀함수 구현에 캐쉬를 추가하는 것으로 지수 시간 복잡도의 함정을 벗어나 의도한 시간 복잡도대로 알고리즘이 작동하도록 만들었습니다. 이 논리를 더 발전시켜 재귀함수를 사용하지 않고 동일한 알고리즘을 구현하는 방법에 대해 알아봅시다.

재귀함수 구현은 기본적으로 크기가 큰 문제에서 작은 문제 쪽으로 이동하는 방법입니다. maxL(N)을 계산하는 과정에서 maxL(N-1)의 값이 필요해지고, 이를 계산하기 위해 재귀함수를 호출하고, … 와 같은 과정이 반복됩니다. 생각을 반대로 뒤집어 크기가 작은 문제부터 차례대로 계산할 수 있습니다. 다시 maxL 함수의 점화식을 보겠습니다.

maxL(n) = max( maxL(i) | i < n and b[i] < b[n] )

maxL(n)이 참조하는 maxL(i)는 항상 i가 n보다 작습니다. 따라서 maxL(1), maxL(2), ..., maxL(N) 순서대로 계산하면, maxL(n)을 계산할 때 항상 필요한 값들을 이미 알고 있기 때문에 재귀함수를 호출하는 작업을 할 필요가 없습니다.

# b = [ ... ]
# maxL = [ ... ]
for n in range(1, N + 1):
    m = 0
    for i in range(1, n):
        if b[i - 1] < b[n - 1]:
            m = max(m, maxL[i])
    maxL[n] = m + 1

앞 섹션에서 재귀함수를 사용한 의사코드에서는 maxL(i) 값을 구할 때 재귀함수 maxL(i) 를 호출했다면, 여기에서는 그냥 리스트에서 값을 maxL[i]로 $O$(1)$$만에 참조하고 있습니다. 그럼에도 불구하고, maxL 값을 올바른 순서에 따라 차례대로 계산하기 때문에 잘 작동합니다.

다른 예시로, 피보나치 수열을 재귀함수로 구현하는 것과 반복문으로 구현하는 것의 차이를 살펴보겠습니다. 두 구현 모두 동일한 점화식 f(n) = f(n-1) + f(n-2)를 사용합니다. 그러나, 우리가 원하는 값 f(N)을 계산하기 위해 접근하는 방식에는 차이가 있습니다.

• 재귀함수:
  • 점화식: f(N) = f(N-1) + f(N-2)
  • f(N-1) 값 계산을 위해 재귀함수 호출
    • f(N-1) = f(N-2) + f(N-3)
      • …
    • f(N-2) = f(N-3) + f(N-4)
      • …
• 반복문:
  • f(3) = f(1) + f(2) = 2
  • f(4) = f(2) + f(3) = 3
  • f(5) = f(3) + f(4) = 5
  • …
  • f(N-1) = f(N-2) + f(N-3) = ??
  • f(N)= f(N-1) + f(N-2) = ??

재귀함수는 위(크기가 큰 문제)에서 아래(크기가 작은 문제)로, 반복문은 아래에서 위로 접근하는 문제 풀이 전략이라는 것이 잘 이해되나요? 두 방법 중 어느 방법을 사용해도 상관 없으나, 사람에 따라 어떤 풀이가 좀 더 잘 이해되는지에는 차이가 있습니다. 그러나, 일반적으로 같은 점화식을 재귀함수와 반복문을 통해 구현하면 시간 복잡도에는 차이가 없으나, 반복문을 통한 구현이 약간 더 빠릅니다. 이는 재귀함수 구현의 실행 시간에는 함수를 호출하는 데 필요한 비용이 추가되는데 비해 반복문 구현에서는 함수를 호출할 필요가 없기 때문입니다. 따라서, 재귀함수 구현과 반복문 구현이 같은 방법이라는 것을 이해하고 서로 자유롭게 전환할 수 있는 방법을 이해하는 것이 중요하겠습니다.