전깃줄 I (wire)
2019.10.27문제
두 전봇대 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생했다. 합선의 위험이 있어 이 중 몇 개를 없애 전깃줄이 교차하지 않도록 만들려고 한다. (두 전깃줄이 전봇대의 동일한 위치에 연결되는 경우는 없다.) 전깃줄의 개수와 전깃줄이 두 전봇대에 연결되는 위치가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하시오.
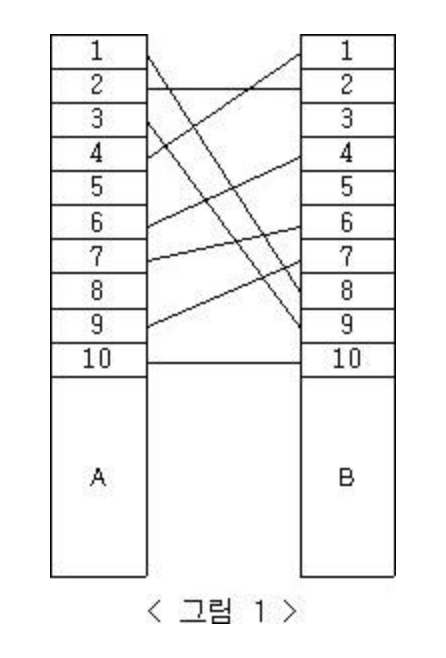
예시
<그림 1>과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다. 이 방법이 최적의 방법이므로 정답은 3개.
관찰
먼저, 두 전깃줄이 교차하기 위한 조건에 대해 생각해 봅시다. 전깃줄을 전봇대에 연결된 위치의 순서쌍 (a, b)로 나타내면, 두 전깃줄 (a1, b1)과 (a2, b2)가 교차하기 위한 조건은 다음과 같습니다.
a1 < a2인 경우,b1 > b2a1 > a2인 경우,b1 < b2
따라서, 문제를 간단하게 하기 위해 N개의 전깃줄을 a가 증가하는 순서대로 정렬하는 전처리를 생각해 볼 수 있습니다. 이렇게 하면 위의 조건에서 두 번째 경우가 배제됩니다. 따라서, 정렬 후 i번째 전깃줄과 j번째 전깃줄이 교차할 조건은 (i < j 일때) b[i] > b[j] 입니다. 전처리를 한 후에는 a를 고려하지 않고, b만 생각해도 전깃줄의 교차 여부를 확인할 수 있습니다.
이제 전깃줄을 b의 리스트 [ b[1], ..., b[N] ]으로 나타내면, 전처리에 의해 이 문제는 이 리스트에서 최소 개수의 숫자를 없애 교차하는 전깃줄이 없도록, 즉 리스트가 오름차순이 되도록 만드는 문제가 됩니다. 이러한 문제를 최대 증가 부분 수열 (Longest Increasing Subsequence, LIS) 문제라고 부릅니다.
이 문제는 크게 두 가지 방법으로 접근할 수 있습니다. 먼저 여러 가지 문제를 다루면서 접해보았던 방법인 답에 관한 이분탐색을 고려해 봅시다. 만약 k개의 전깃줄을 없애 남은 전깃줄을 모두 교차하지 않게 만들 수 있다면, 당연히 k개 이상의 전깃줄을 없애는 것도 가능하기 때문에 LIS 문제에서 이 방법을 사용할 수 있습니다.
다른 접근 방법으로는 재귀함수를 사용할 수 있습니다. 재귀함수를 사용하여 문제를 해결하기 위한 조건은 기존 문제와 크기를 더 줄인 문제의 답 간에 관계가 존재해야 한다는 것입니다.
두 가지 문제 풀이 방법을 다음 섹션에서 각각 고려해 보고, 어떤 방법이 더 좋은 방법인지 시간 복잡도를 통해 평가해 보도록 하겠습니다.
풀이
답에 관한 이분탐색
없애야 하는 전깃줄의 개수는 0개부터 N-1개까지 총 N가지 경우가 있습니다. “답에 관한 이분탐색” 접근에 관해 모르는 상태였다면, N가지 경우를 모두 시험해 보아야 했을 것입니다. 그러나, k개의 전깃줄을 제거해 어느 전깃줄도 교차하지 않는 상태를 만들 수 있다면, k개 이상의 전깃줄을 제거해도 그 상태를 만들 수 있기 때문에 제거할 전깃줄의 개수를 이분탐색하여 log N번만 시험해 보아도 됩니다.
그런데, k개의 전깃줄을 없앴을 때 어느 두 전깃줄도 교차하지 않는 상태를 만들 수 있는지 여부를 빠르게 판단하는 문제가 아직 남아 있습니다. 마찬가지로, 모든 경우를 시험해 보는 방법의 시간복잡도부터 알아보겠습니다. N개의 전깃줄 중 k개를 고르는 경우의 수는 총 \(_{N}C_{k}\) 가지이며, 없앨 전깃줄을 고른 상태에서 교차하는 전깃줄이 있는지 알아보는 과정에서는 길이 N-k의 리스트를 순회해야 합니다. 따라서, 시간 복잡도는 \(O(N^N)\) 또는 \(O(2^{N log N})\) 으로 상당히 높으므로 이 방법으로 접근해서는 문제를 풀기 어렵습니다.
재귀함수 정의하기
없앨 k개의 전깃줄을 정하는 경우를 일일이 고려하지 않는 방법에는 어떤 방법이 있을까요? 이러한 방법도 생각해 볼 수 있습니다. 앞에서부터 (즉, a[i]가 작은 전깃줄부터) 차례대로 전깃줄을 고려하면서, 이미 고른 전깃줄과 겹치지 않는 전깃줄이면 추가하고, 겹치는 전깃줄이면 없애는 것입니다. 예시로, (전처리 후의) 전깃줄을 차례로 [2, 4, 7, 5, 8] 이라고 하면, 2, 4, 7을 차례로 고른 후 5는 7 전깃줄과 겹치므로 고르지 않습니다. 그리고 8을 마지막으로 고르면 1개의 전깃줄을 고르지 않고 (즉, 제거하고) 겹치지 않는 상태를 만들 수 있습니다.
그러나, 이렇게 무조건 앞에서부터 전깃줄을 고르는 것은 근시안적인 방법입니다. 예시의 상황처럼 전깃줄이 [8, 2, 9, 1, 4, 6, 7, 10] 8개가 있다면, 맨 처음에 8 전깃줄을 고르는 결정으로 인해 뒤의 2, 1, 4, 6, 7 5개나 되는 전깃줄을 고르지 못하는 상황이 생깁니다.
많은 문제에서 근시안적인 결정, 또는 욕심쟁이 알고리즘 (Greedy Algorithm) 에 관한 딜레마에 접하게 됩니다. 대부분의 문제에서 근시안적인 결정만 해서는 문제를 해결할 수 없고, 미래의 선택까지 고려해서 효율적인 결정을 해야 최적의 답을 찾을 수 있습니다. 모든 경우를 빠르게 고려하는 데 도움을 주는 도구가 바로 재귀함수입니다.
재귀함수로 문제를 풀기 위해 재귀함수 f(n)을 정의합시다. 여기에서 f(n) = "n개의 전깃줄에서 모든 전깃줄이 교차하지 않는 상태를 만들기 위해 제거해야 하는 전깃줄의 최소 개수" 입니다. 예시에서 주어진 전깃줄 [8, 2, 9, 1, 4, 6, 7, 10]으로 예를 들어보면, 다음 표와 같습니다.
n |
전깃줄 | f(n) |
제거하는 전깃줄 | 남아있는 전깃줄 |
|---|---|---|---|---|
1 |
[8] |
0 |
- |
[8] |
2 |
[8, 2] |
1 |
2 |
[8] |
3 |
[8, 2, 9] |
1 |
2 |
[8, 9] |
4 |
[8, 2, 9, 1] |
2 |
2, 1 |
[8, 9] |
5 |
[8, 2, 9, 1, 4] |
3 |
2, 1, 4 |
[8, 9] |
6 |
[8, 2, 9, 1, 4, 6] |
3 |
8, 2, 9 |
[1, 4, 6] |
7 |
[8, 2, 9, 1, 4, 6, 7] |
3 |
8, 2, 9 |
[1, 4, 6, 7] |
8 |
[8, 2, 9, 1, 4, 6, 7, 10] |
3 |
8, 2, 9 |
[1, 4, 6, 7, 10] |
여기에서 f(5)에서 f(6)으로 넘어가는 과정에 유의하세요. f(1) ~ f(5) 까지는 8 전깃줄을 고르고 거기에서부터 오름차순 순열 [8, 9, ...] 을 만들어 나갈 것처럼 보이다가, 갑자기 f(6)에서 [1, 4, 6, ...] 순열로 진행합니다. 이러한 결정이 가능하도록 하기 위해서는 f(5)를 계산하는 과정에서 최적 [8, 9] 외에도 [1, 4]라는 오름차순 순열이 존재한다는 것을 기억했다가, 6번째 전깃줄 6이 등장했을 때 [8, 9] 다음에는 6이 오지 못하지만, [1, 4] 다음에는 올 수 있으므로 최적의 순열을 [1, 4, 6]으로 바로 교체해야 합니다. 따라서 우리는 블랙잭 문제에서처럼 재귀함수를 다시 정의해야 한다는 것을 알 수 있습니다.
IS(n) = n개의 전깃줄에서 만들 수 있는 모든 오름차순 순열
n |
IS(n) |
|---|---|
1 |
[ [8] ] |
2 |
[ [8], [2] ] |
3 |
[ [8], [2], [9], [8, 9], [2, 9] ] |
4 |
[ [8], [2], [9], [8, 9], [2, 9], [1] ] |
5 |
[ [8], [2], [9], [8, 9], [2, 9], [1], [4], [2, 4], [1, 4] ] |
6 |
[ [8], [2], [9], [8, 9], [2, 9], [1], [4], [2, 4], [1, 4], [6], [2, 6], [1, 6], [4, 6], [2, 4, 6], [1, 4, 6] ] |
7 |
[ [8], [2], [9], [8, 9], [2, 9], [1], [4], [2, 4], [1, 4], [6], [2, 6], [1, 6], [4, 6], [2, 4, 6], [1, 4, 6], [7], [2, 7], [1, 7], [4, 7], [2, 4, 7], [1, 4, 7], [6, 7], [2, 6, 7], [1, 6, 7], [4, 6, 7], [2, 4, 6, 7], [1, 4, 6, 7] ] |
8 |
[ [8], [2], [9], [8, 9], [2, 9], [1], [4], [2, 4], [1, 4], [6], [2, 6], [1, 6], [4, 6], [2, 4, 6], [1, 4, 6], [7], [2, 7], [1, 7], [4, 7], [2, 4, 7], [1, 4, 7], [6, 7], [2, 6, 7], [1, 6, 7], [4, 6, 7], [2, 4, 6, 7], [1, 4, 6, 7], [10], [8, 10], [2, 10], [9, 10], [8, 9, 10], [2, 9, 10], [1, 10], [4, 10], [2, 4, 10], [1, 4, 10], [6, 10], [2, 6, 10], [1, 6, 10], [4, 6, 10], [2, 4, 6, 10], [1, 4, 6, 10], [7, 10], [2, 7, 10], [1, 7, 10], [4, 7, 10], [2, 4, 7, 10], [1, 4, 7, 10], [6, 7, 10], [2, 6, 7, 10], [1, 6, 7, 10], [4, 6, 7, 10], [2, 4, 6, 7, 10], [1, 4, 6, 7, 10] ] |
위의 표를 보면 알 수 있듯이, IS(n)을 계산하는 것에는 큰 문제가 있습니다. 앞 섹션에서 고려했던 것처럼 모든 경우를 고려하는 것과 별로 차이가 없기 때문입니다. 경우의 수는 2N가지 존재할 수 있기 때문에 IS(N) 리스트의 길이는 매우 길며, 시간 복잡도도 마찬가지로 지수 시간( \(O(2^N)\) )입니다.
IS(n)에 들어 있는 순열들 중에는 고려할 필요가 없는 것들도 있습니다. 예를 들어, IS(6)에는 [4, 6] 순열이 들어 있습니다. 그러나, 우리는 이미 IS(5)에 들어있는 [2, 4], [1, 4] 순열을 통해 4 전깃줄 앞에는 2, 1 등 더 많은 전깃줄이 올 수 있음을 알고 있기 때문에 [4, 6] 순열은 필요가 없습니다. ([2, 4, 6]과 [1, 4, 6] 순열이 이 경우를 이미 고려해주고 있습니다.) 이 점을 고려하여 다시 함수를 정의해 봅시다.
LIS(n) = n개의 전깃줄에서 만들 수 있는 모든 오름차순 순열 중, 최대한 길이를 늘린 순열
n |
LIS(n) |
|---|---|
1 |
[ [8] ] |
2 |
[ [8], [2] ] |
3 |
[ [8, 9], [2, 9] ] |
4 |
[ [8, 9], [2, 9], [1] ] |
5 |
[ [8, 9], [2, 9], [2, 4], [1, 4] ] |
6 |
[ [8, 9], [2, 9], [2, 4, 6], [1, 4, 6] ] |
7 |
[ [8, 9], [2, 9], [2, 4, 6, 7], [1, 4, 6, 7] ] |
8 |
[ [8, 9, 10], [2, 9, 10], [2, 4, 6, 7, 10], [1, 4, 6, 7, 10] ] |
리스트가 굉장히 깔끔해졌습니다. 더 줄일 수 있는 방법도 있습니다. LIS(5)에서 LIS(6)으로 갈 때 [2, 4]와 [1, 4]가 각각 [2, 4, 6]과 [1, 4, 6]으로 변하는데, 사실 두 경우를 모두 고려할 필요가 없습니다. [2, 4]와 [1, 4]는 모두 4로 끝나고, 길이가 2이기 때문에 여기에 6 전깃줄을 추가하여 길이 3의 오름차순 순열이 되는 것은 동일하기 때문입니다. 즉, 오름차순 순열 그 자체보다는 마지막 숫자와 그 길이만 고려하면 된다는 중요한 인식을 가질 수 있습니다.
maxL(n) = n번째 전깃줄로 끝나는 오름차순 순열의 최대 길이
n |
maxL(n) |
오름차순 순열 예시 (LIS(n)과 비교해 보세요.) |
|---|---|---|
1 |
1 |
[8] |
2 |
1 |
[2] |
3 |
2 |
[8, 9], [2, 9] |
4 |
1 |
[1] |
5 |
2 |
[2, 4], [1, 4] |
6 |
3 |
[2, 4, 6], [1, 4, 6] |
7 |
4 |
[2, 4, 6, 7], [1, 4, 6, 7] |
8 |
5 |
[2, 4, 6, 7, 10], [1, 4, 6, 7, 10] |
없애야 할 전깃줄의 개수는 f(N) = N - max( maxL(1), ..., maxL(N) )으로 쉽게 구할 수 있습니다.
재귀함수 구현
이제 재귀함수 maxL(n)을 구현해 봅시다. 많은 문제들에서 다뤘듯이, 두 가지 점에 관해 생각합니다.
- 가장 기본적인 경우:
maxL(1)은 무엇인가? ⇒maxL(1) = 1 - 더 작은 문제와의 관계
maxL(n)과maxL(n-1)만 생각해서는 관계를 찾기 어렵습니다.maxL(n)을 계산하기 위해 사용할 수 있는 값들에는 더 작은 문제의 값maxL(1), maxL(2), ..., maxL(n-1)까지 있기 때문에 이들을 모두 활용해야 합니다.maxL(n)의 정의를 생각해 보면,n번째 전깃줄로 끝나는 오름차순 순열을 고려하고 있습니다. 오름차순 순열의 맨 마지막에b[n]이 오려면 그 이전 숫자는b[n]보다 작아야 합니다. 따라서 고려해야 하는maxL(i)들은b[i]가b[n]보다 작은i들입니다.- 이 중에서 최대 길이를 구해야 하므로, 위의 조건을 만족하는
i들 중maxL(i)가 가장 큰 것을 찾아야 합니다. 따라서maxL(n) = max( maxL(i) | i < n and b[i] < b[n] ) + 1, 만족하는i가 없으면 그냥maxL(n) = 1.
예시로, 다시 b = [8, 2, 9, 1, 4, 6, 7, 10]일 때를 생각해 보면,
maxL(1) = 1maxL(2) = 1maxL(3) = max( maxL(1), maxL(2) ) + 1 = 2maxL(4) = 1maxL(5) = max( maxL(2), maxL(4) ) + 1 = 2maxL(6) = max( maxL(2), maxL(4), maxL(5) ) + 1 = 3maxL(7) = max( maxL(2), maxL(4), maxL(5), maxL(6) ) + 1 = 4maxL(8) = max( maxL(1), maxL(2), maxL(3), maxL(4), maxL(5), maxL(6), maxL(7) ) + 1 = 5
maxL(N)을 구하는 데 필요한 시간 복잡도를 계산해 봅시다. 식 하나 maxL(n) = max( maxL(i) ) + 1를 계산하는 데 필요한 시간 복잡도는 \(O(N)\)입니다. (조건을 만족하는 i가 최대 n-1개 있을 수 있으므로) 이러한 식을 maxL(1), ..., maxL(N)까지 총 N번 계산해야 하므로, 최종 결과 maxL(N)을 구하기 위해서는 \(O(N^2)\)의 시간 복잡도가 소요됩니다.
입력 및 출력 예제
입력 형식
- 첫 번째 줄에는 전깃줄의 개수
N이 주어진다. (1 <= N <= 100) - 두 번째 줄부터
N개의 줄에 전깃줄을 연결할 두 위치a[i], b[i]가 주어진다. (1 <= a[i], b[i] <= 500, 모든a[i]와 b[i]끼리는 서로 다르다.)
출력 형식
남아있는 모든 전깃줄이 교차하지 않도록 하기 위해 제거해야 할 전깃줄의 최소 개수를 출력한다.
입력 예제 1
8
1 8
3 9
2 2
4 1
6 4
10 10
9 7
7 6
출력 예제 1
3
원문
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, <그림 1>과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.

전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
출처
- 한국정보올림피아드, 지역본선 2007 초등부 4번 (전깃줄)