기지국 (stations)
2019.05.05문제
최근 개발된 5G 등, 광역 무선 연결망이 작동하기 위해서는 통신사들이 전국 각지에 기지국을 설치하여 무선 기기들이 네트워크에 접속할 수 있도록 해야 한다. 또, 기지국들이 서로 통신망으로 연결되어 있어야 멀리 떨어진 사람들의 통신을 중계할 수 있다.
두 기지국이 서로 연결되기 위해서는 기지국에 놓이는 통신 장비의 성능이 충분해야 한다. 물론, 강력한 장비를 놓을수록 멀리 떨어진 기지국들이 직접 통신할 수 있지만, 그만큼 비싸기 떄문에 통신 장비의 유효 거리를 최소화하면서 모든 기지국들을 서로 연결시키고자 한다.
N개의 기지국들의 위치가 주어졌을 때, 모든 기지국들이 서로 연결되기 위한 통신 장비의 최소 유효 사거리를 구하시오.
예시
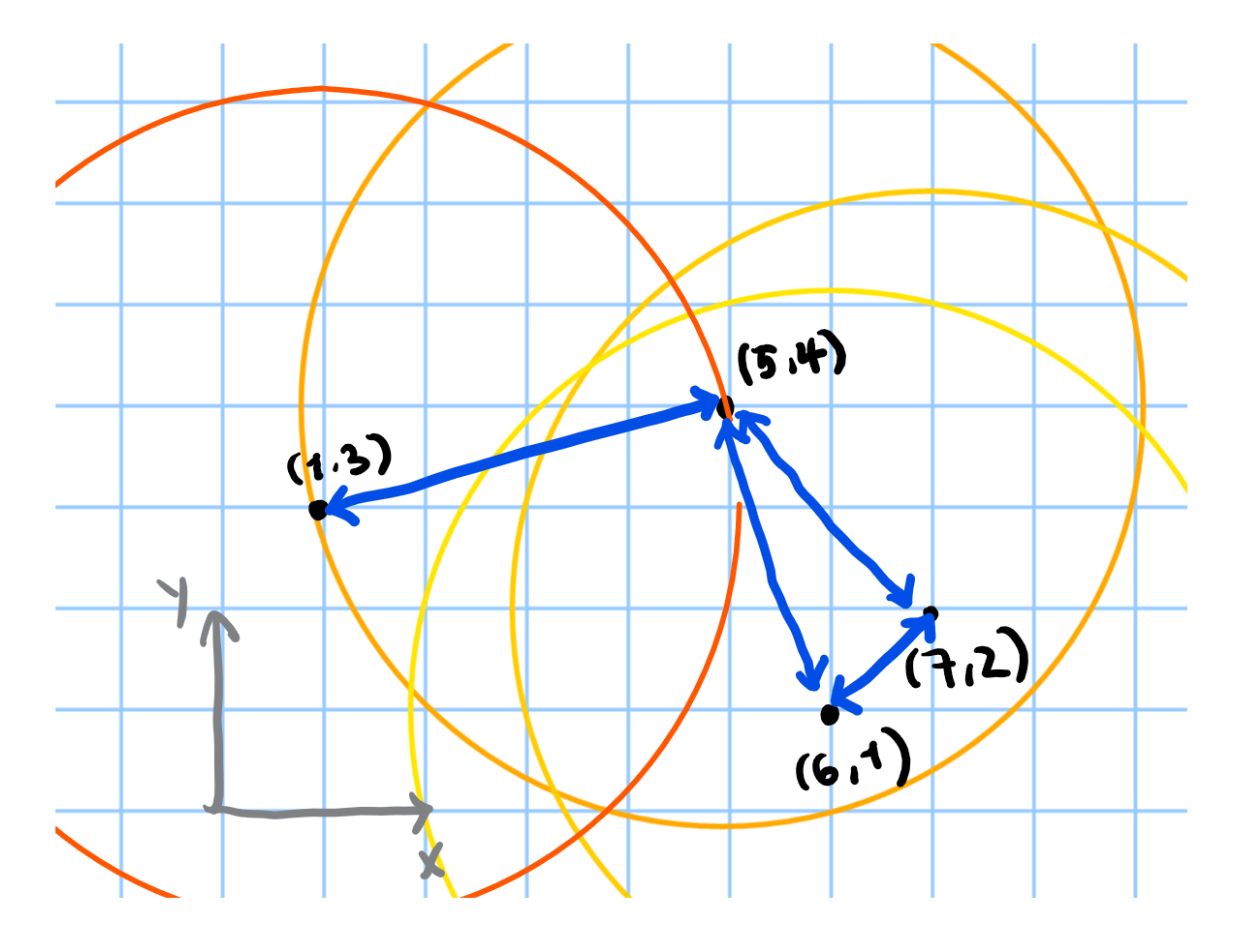
4개의 기지국이 (1, 3), (5, 4), (6, 1), (7, 2)의 위치에 있다고 하자. 위 그림처럼, 통신 장비의 사거리를 sqrt(17)로 하면 모든 기지국을 서로 연결할 수 있다. (1, 3) 기지국과 (6, 1) 기지국은 직접 통신할 수는 없지만, (5, 4) 기지국을 통해 서로 연결됨에 유의하라.
관찰
모든 기지국에 놓이는 통신 장비의 유효 거리가 동일하기 때문에, 사거리를 0부터 시작하여 점점 늘려가면서 기지국들을 하나하나 연결해 가는 전략을 생각해 볼 수 있습니다. 즉, 문제에서 제시한 예시에 적용해 보면 이렇습니다.
| 유효 거리 | 상태 |
|---|---|
| 0 | (처음 상태) |
| … | |
| sqrt(2) | (6, 1)과 (7, 2) 기지국이 직접 연결됨 |
| … | |
| sqrt(8) | (7, 2)와 (5, 4) 기지국이 직접 연결됨 |
| … | |
| sqrt(10) | (6, 1)과 (5, 4) 기지국이 직접 연결됨 |
| … | |
| sqrt(17) | (1, 3)과 (5, 4) 기지국이 직접 연결됨, 이때 모든 기지국이 서로 연결됨. |
모든 기지국이 연결되었다면 그 때의 유효 거리가 바로 정답이 됩니다.
따라서, 이 전략을 알고리즘으로 구현하기 위해서는 두 기지국 간의 거리를 정렬하고, 서로 가까운 기지국들부터 확인하며
- 두 기지국을 서로 직접 연결하는 연산
- 모든 기지국이 연결되었는지 확인
을 번갈아 진행하면 되겠습니다.
풀이
Union-Find 자료구조를 이용한 풀이
앞서 다뤘던 문제들과 마찬가지로,
- 두 집합을 서로 합치는 연산
- 원소가 어떤 집합에 있는지? 집합의 크기가 얼마인지? 등의 질의
이와 같은 연산들을 빠르게 처리할 수 있는 Union-Find 자료구조를 통해 이 문제를 해결할 수 있습니다.
즉,
- 두 기지국 x, y를 서로 연결하는 연산:
Union(x, y) - 모든 기지국이 서로 연결되었는지?: 아무 기지국 x에 대해,
Find(x)의 크기가 N인지?
를 판단하는 것으로 간단히 문제를 해결할 수 있습니다. Union-Find 자료구조는 Union과 Find 연산을 상수 시간 복잡도 O(1)에 처리할 수 있습니다. 두 기지국의 쌍은 총 N(N-1)/2개가 존재하므로, 처음에 두 기지국 간의 거리를 정렬하는 연산은 O(N^2 log N)의 시간 복잡도를, 이후 두 기지국 간의 거리를 가까운 것부터 확인하며 Union과 Find 연산을 한 번씩 수행하는 것은 최대 O(N^2)의 시간 복잡도가 필요합니다. 따라서, 최종적인 시간 복잡도는 O(N^2 log N)입니다.
더 알아보기: 최소 신장 트리(Minimum Spanning Tree)
이 문제는 최소 신장 트리를 찾아내는 대표적인 문제입니다. 최소 신장 트리란, 그래프에서 모든 정점을 연결하는 트리 중 가장 비용이 낮은 트리를 말합니다. 이 문제에서 사용한 전략인, 두 기지국의 거리가 가장 가까운 순서대로 연결하면서, 모든 기지국이 서로 연결될 때까지 진행하는 알고리즘은 최소 신장 트리 문제에 대한 유명한 해법입니다. 이 알고리즘에게는 Kruskal 알고리즘이라는 이름도 있습니다.
그렇다면 Kruskal 알고리즘이 최소 신장 트리 문제에 대한 유일한 해법일까요? 그렇지 않습니다. 다른 해법은 Prim 알고리즘이라고 부르는데, 이 또한 Kruskal 알고리즘과 동일한 시간 복잡도를 가집니다. Kruskal 알고리즘은 전체 기지국들 중 가장 가까운 기지국들을 연결해 나가는 전략을 사용합니다.
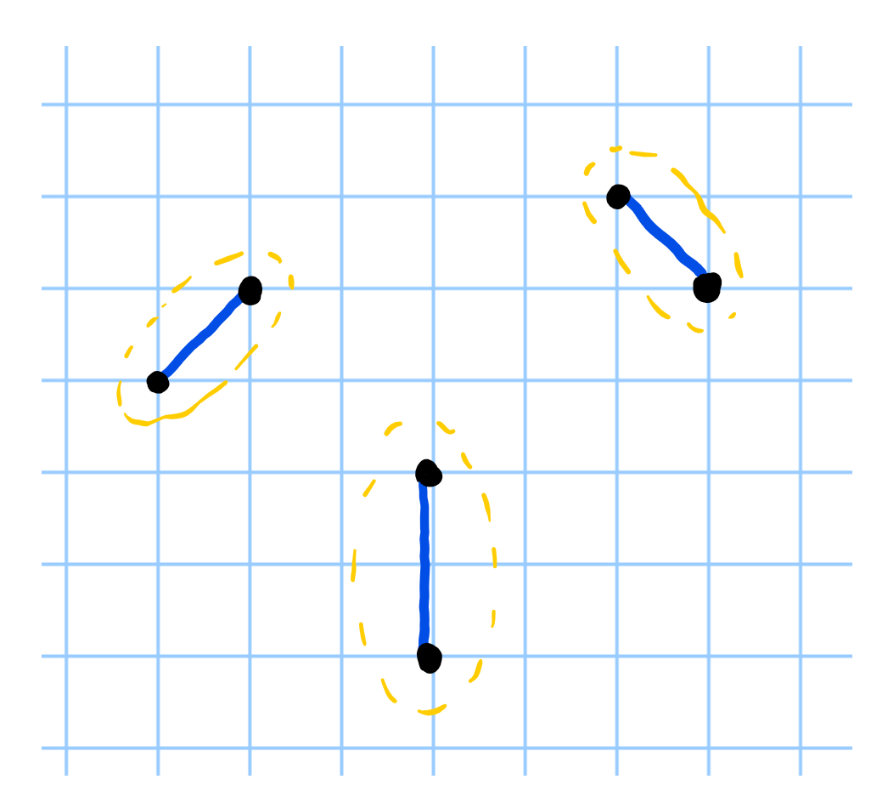
그러나, Prim 알고리즘은 한 기지국에서 출발하여, 가장 가까운 기지국을 계속해서 찾아가 연결하는 전략을 사용합니다.
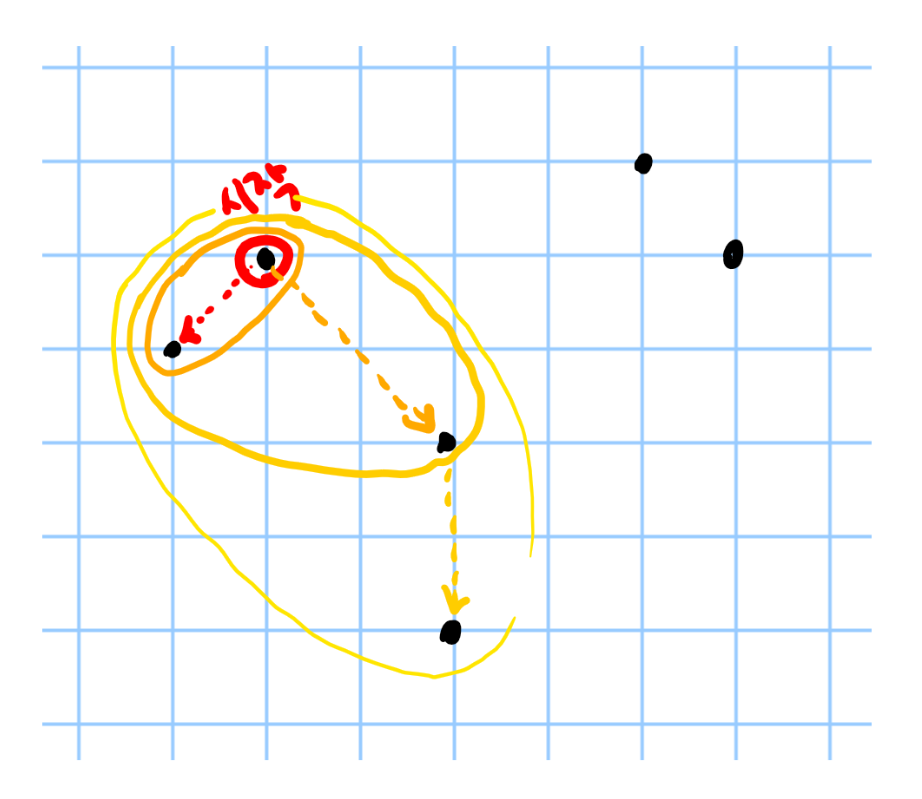
- 아무 기지국에서 출발한다.
- 모든 기지국들이 연결될 때까지, 현재 연결된 기지국들에서 가장 가까운 아직 연결되지 않은 기지국을 골라 연결한다.
이와 같이 진행했을 때 필요한 통신 장비의 사거리가 마찬가지로 정답이 됩니다. 다만, 현재 연결된 기지국에서 가장 가까운 기지국을 찾는 것을 효율적으로 진행해야 Union-Find 자료구조를 사용하는 Kruskal 알고리즘과 같은 시간 복잡도를 얻을 수 있습니다. 이는 이 문제에서는 자세히 다루지는 않도록 하겠습니다.
더 알아보기: 평면상에서의 최소 신장 트리
이 문제에서 시간 복잡도가 증가하는 원인은, 모든 N(N-1)/2개의 기지국 쌍 간의 거리를 유효 사거리의 후보로 고려하기 때문입니다. 하지만, 정말 그렇게 할 필요가 있을까요? 예를 들어, 어떤 두 기지국이 굉장히 멀리 떨어져 있고 그 사이에 다른 기지국들이 충분히 많다면 (그리고 다른 기지국들이 있다는 것을 쉽게 체크할 수 있다면), 후보에서 제외함으로서 전처리 정렬 시간 O(N^2 log N)을 줄일 수 있을 것입니다.
실제로, 2차원 평면 상에서 유클리드 거리를 사용하는 경우에 대해 어떤 점으로부터 가까운 점들을 찾는 여러 가지 최적화 기법이 있습니다. 궁금하신 분들은 다음 내용을 참고하시면 좋겠습니다.
- Voronoi Diagram
- k-d Tree
입력/출력 예제
입력 형식
- 첫 번째 줄에는 기지국의 개수 N이 입력된다. (1 <= N <= 1,000)
- 다음 N개의 줄에는 각 기지국의 위치 x, y가 입력된다. (0 <= x, y <= 25,000)
출력 형식
- 모든 기지국이 연결되는 통신 장비의 최소 유효 사거리의 제곱을 출력한다.
입력 예제 1
4
1 3
5 4
7 2
6 1
출력 예제 1
17
원문
Farmer John’s N cows (1≤N≤1000) want to organize an emergency “moo-cast” system for broadcasting important messages among themselves.
Instead of mooing at each-other over long distances, the cows decide to equip themselves with walkie-talkies, one for each cow. These walkie-talkies each have a limited transmission radius, but cows can relay messages to one-another along a path consisting of several hops, so it is not necessary for every cow to be able to transmit directly to every other cow.
The cows need to decide how much money to spend on their walkie-talkies. If they spend $X, they will each get a walkie-talkie capable of transmitting up to a distance of sqrt(X). That is, the squared distance between two cows must be at most X for them to be able to communicate.
Please help the cows determine the minimum integer value of X such that a broadcast from any cow will ultimately be able to reach every other cow.
출처
USA Computing Olympiad, 2006 December Contest, Gold, Problem 1 (moocast)