불꽃놀이 (fireworks)
2019.04.30문제
여의도에서 열리는 불꽃축제에는 매년 수많은 사람들이 몰린다. 하늘에서 다양한 색깔의 불꽃이 터지는 광경을 사진으로 남기면 정말 멋있지 않을까?
하늘에 N개의 불꽃이 동시에 터질 때, M명의 사진가들이 사진을 찍었다. 각 사진은 서로 다른 각도에서 촬영되었기 때문에, N개의 불꽃 중 일부만을 담고 있다. 그러나, 사진에 같은 색깔의 불꽃이 너무 많으면 단조롭기 때문에 같은 색의 불꽃이 절반보다 많이 담겨 있는 사진을 구별하고자 한다. N개의 불꽃 색깔과 M장의 사진들이 주어질 때, 단조로운 사진을 구별하는 알고리즘을 생각해 보자.
- 불꽃의 색깔은 총 C가지가 존재한다.
예시
N=10개의 불꽃이 터지고 각각의 색깔이 다음과 같다고 하자. (서로 다른 숫자는 서로 다른 색을 나타낸다.)
[1, 2, 1, 2, 1, 2, 3, 2, 3, 3]
사진 M=4장이 다음과 같이 주어질 때, 각 사진의 단조로움을 판단해 보자.
- 1~2 번째 불꽃을 담고 있는 사진은 전체의 절반(1개)보다 많이 차지하는 색깔이 없기 때문에 (1번 색 1개, 2번 색 1개) 단조롭지 않다.
- 2~4 번째 불꽃을 담고 있는 사진은 2번 색 불꽃이 전체의 절반(1.5개)보다 많이 있기 때문에 단조롭다.
- 6~9 번째 불꽃을 담고 있는 사진은 전체의 절반(2개)보다 많이 차지하는 색깔이 없기 때문에 (2번 색 2개, 3번 색 2개) 단조롭지 않다.
- 7~10번째 불꽃을 담고 있는 사진은 3번 색 불꽃이 전체의 절반(2개)보다 많이 있기 때문에 단조롭다.
관찰
가장 단순한 풀이는 사진이 주어질 때마다 사진에 속하는 불꽃을 전부 체크하여 색깔별로 불꽃의 갯수를 세고, 그 중 절반이 넘는 색깔이 존재하는지 검사하는 것입니다.
# firework_colors: N개의 불꽃 색깔을 담고 있는 리스트.
# 색은 1~C의 숫자로 표현된다.
# photos: M개의 사진에 대한 정보를 (s, e) 형태로 담고 있는 리스트.
# i번째 사진에는 s~e번째 불꽃이 등장한다.
def solution(firework_colors, photos):
ret = []
for (s, e) in photos:
# 리스트를 초기화한다.
colors_in_photo = [0] * C
# s~e번째 불꽃을 보면서 각 색깔이 몇 번 나왔는지 기록한다.
for i in range(s, e + 1):
colors_in_photo[firework_colors[i]] += 1
# 색깔 중 절반 넘게 존재하는 색이 있는지 확인한다.
dominant_color = -1
for color in range(C):
if colors_in_photo[color] > (e - s + 1) / 2:
dominant_color = color
ret.append(dominant_color)
return ret
이 풀이의 시간 복잡도는 어떻게 될까요? 사진이 M장 있고, 사진마다 최대 N개의 불꽃을 체크하며, 체크한 후에는 최대 C개의 색깔 중 절반 이상 존재하는 색이 있는지 알아내야 하므로, 시간복잡도는 O(M(N+C))가 됩니다.
풀이
누적 합의 활용
위의 풀이에서 s~e번째 불꽃을 보는 과정은 누적 합이라는 단순한 방법을 통해 시간 복잡도를 줄일 수 있습니다. 다음과 같은 문제를 생각해 봅시다.
“주어진 배열에서, s~e번째 숫자들의 합을 구하시오.”
이러한 질의(query, 쿼리)가 한 번만 주어진다면, s~e번째 숫자들을 일일이 보면서 더하는 방법으로 해결할 것입니다. 하지만, 서로 다른 범위에서 합을 구하는 질의가 여러 번 주어진다면 그 때마다 다시 숫자들을 더하는 것이 비효율적이라는 것을 알 수 있습니다. 예시로 배열 [3, 1, 4, 1, 5, 9, 2]가 주어졌을 때, 다음과 같이 새로운 배열을 만들어 봅시다.
| 원래 배열 | 3 | 1 | 4 | 1 | 5 | 9 | 2 |
|---|---|---|---|---|---|---|---|
| 새로운 배열 | 3 | 4 | 8 | 9 | 14 | 23 | 25 |
새로운 배열은 누적 합 배열로, 원래 배열의 합을 계속해서 더해 나간 결과를 저장하고 있습니다. 여러 개의 질의에 대답하기 전 누적 합 배열을 미리 만들어 놓으면, s~e번째 숫자들의 합은 누적 합 배열에서 e번째 숫자에서 s-1번째 숫자를 빼서 계산할 수 있습니다. 수식으로 설명하면 다음과 같이 됩니다.
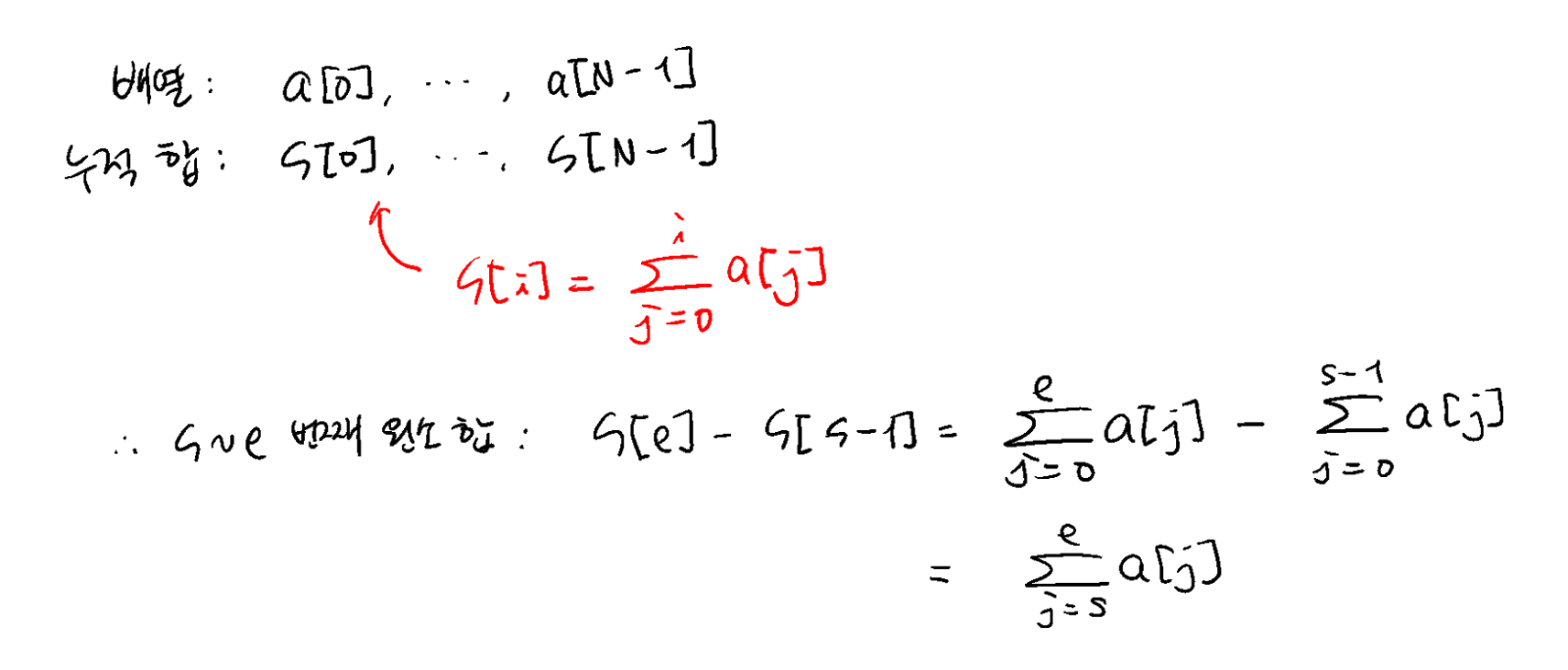
누적 합을 사용하면 시간 복잡도가 어떻게 향상될까요? 배열의 길이가 N이고, 총 M개의 질의가 주어진다고 했을 때, 단순한 방법으로 계산하면 NM번의 연산이 필요합니다. 누적 합을 사용하는 경우, 누적 합 배열을 만드는 데 N번의 연산이 필요하고, 이후 M개의 질의에는 질의 당 한 번의 연산으로 계산할 수 있으니, 총 N+M번의 연산이 필요한 것을 알 수 있습니다. 간단한 처리만으로 시간 복잡도를 O(NM)에서 O(N+M)으로 크게 줄였습니다.
이 문제에서 누적 합을 사용하면 s~e 구간에서 각 색깔이 총 몇 번 등장했는지 쉽게 알 수 있습니다. 각 색깔에 대해, 다음과 같은 배열을 정의해 봅시다.
C[color][i] = i번째 색이 color이면 1, 아니면 0
예를 들어, 위에 주어진 예시 상황에서는 다음과 같습니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 |
이제 s~e 구간에서 color 색이 몇 번 등장했는지 구하는 문제는 C[color] 일차원 배열에서 s~e번째 숫자의 합을 구하는 문제로 변하게 됩니다. 따라서, 방금 설명한 누적 합 배열을 미리 계산해 놓으면 이를 빠르게 계산할 수 있을 것입니다.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 |
| 2 | 0 | 1 | 1 | 2 | 2 | 3 | 3 | 4 | 4 | 4 |
| 3 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 |
누적 합 배열을 만드는 데 총 O(NC)의 시간복잡도가 소요되고, 이제 각 질의를 O(N+C)가 아닌 O(C)의 시간 복잡도로 처리할 수 있으므로 총 시간 복잡도는 O(M(N+C))에서 O(NC + MC) = O((N+M)C)로 변합니다. 다만, 시간 복잡도는 줄어들 수 있어도 NxC 크기의 배열에 누적 합을 저장해야 하므로, 메모리 사용량이 늘어난다는 점을 고려해야 합니다.
버킷
누적 합 배열을 활용하여 특정 색깔의 불꽃이 구간 내에 몇 개가 있는지 빠르게 구할 수는 있지만, 모든 색깔이 절반보다 많이 존재하는 색깔이 될 수 있는 후보가 될 수 있습니다. 따라서 각 사진마다 C개의 색깔을 일일이 확인하여야 하며, 이 부분이 우리의 풀이에서 많은 시간복잡도를 차지하고 있습니다.
우리가 보고 있는 구간을 여러 개로 나눠보면, 다음과 같은 성질을 관찰할 수 있습니다.
“전체 구간에서 절반보다 많이 존재하는 색깔은, 나눠진 구간 중 적어도 하나에서 절반보다 많이 존재하는 색깔이어야 한다.”
만약 어떤 색깔이 모든 부분 구간에서 절반 이하로 존재한다면, 전체 구간에서도 절반 이하를 차지할 수 밖에 없기 때문에 이러한 성질이 성립합니다. 따라서, 미리 잘게 나눠 놓은 구간에 대해 절반보다 많이 존재하는 색깔을 미리 계산해 놓은 뒤, 질의가 들어오면 미리 계산해 놓은 결과를 이용해서 절반 이상 차지할 수 있는 색깔의 후보를 크게 줄일 수 있습니다.
예를 들어, 불꽃이 총 100개일 때 미리 5개씩 나눠 놓은 20개의 소구간에서 3개 이상 차지하는 색깔을 계산해 놓았다고 합시다. 만약 22~89번째 불꽃이 있는 사진이 질의로 들어올 경우, 기존에는 100개의 색깔에 대해 이 구간 내에 몇 개의 불꽃이 있는지를 계산한 후, 그 중 절반보다 많은 색을 찾았습니다. 하지만, 22~89 구간을 다음과 같이 나누면,
(22~25), (26~30), (31~35), … , (81~85), (86~89)
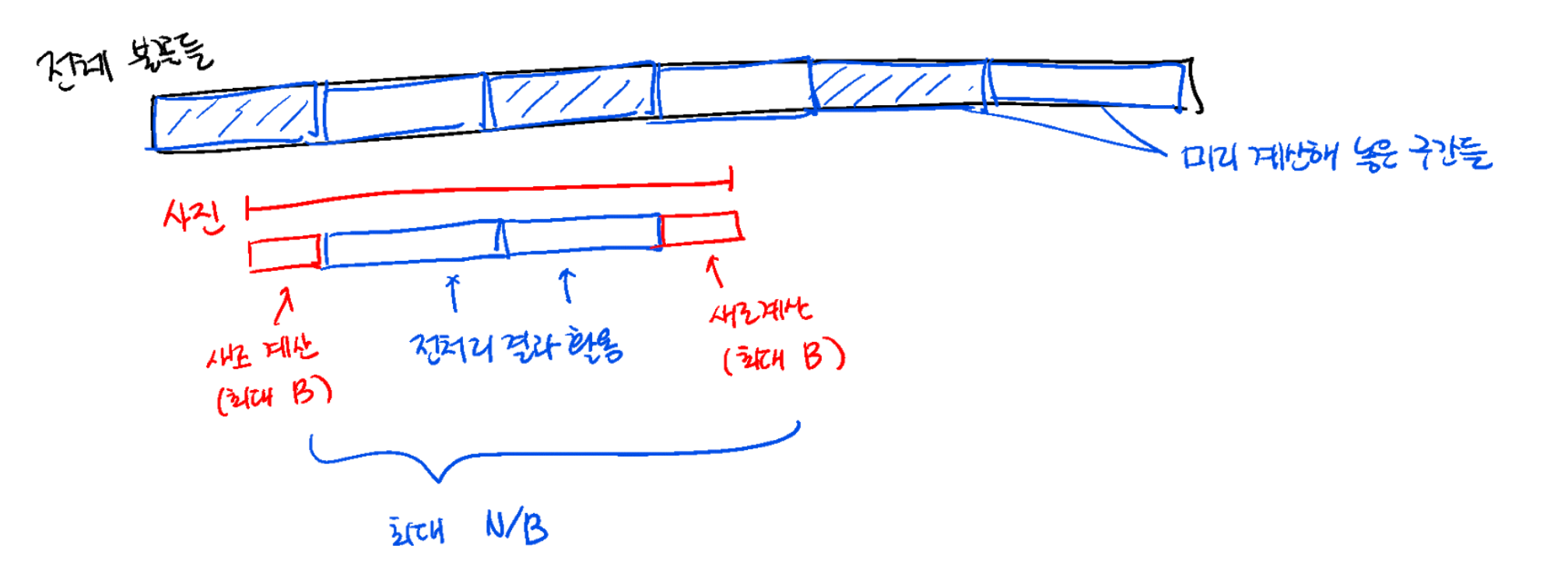
각각의 소구간들에서 절반보다 많은 색깔들만이 후보가 될 수 있으므로, 후보는 100개에서 16개로 줄어듭니다. (26~30) 등 미리 계산해 놓은 소구간은 바로 후보를 알 수 있으므로, 양 끝에 잘린 소구간에 대해서만 절반보다 많은 색깔을 새로 계산하면 됩니다.
정리하면 다음과 같습니다.
-
전처리: 누적 합 배열을 계산하고, N개의 불꽃을 B개씩 들어있는 소구간으로 쪼갠 뒤, 각 소구간에서 B/2개 보다 많은 색깔을 찾아 저장해 둔다.
-
각 사진에 대해서,
- 사진에 포함된 소구간들에서 절반보다 많이 차지하는 색깔을 기록에서 찾아오고, 양 끝에 잘린 구간들에 대해서는 그러한 색깔을 다시 계산한다.
- 위에서 찾은 후보 색들에 대해, 실제로 그 색깔이 이 사진에서 절반 이상 차지하고 있는지 누적 합 배열을 통해 빠르게 찾는다.
이제 이 방법의 시간 복잡도를 계산해 봅시다. 불꽃이 총 N개일 때, 이 불꽃을 대략 B개씩 나눠 N/B개의 소구간을 만든 후, 각각의 소구간에서 절반 이상 존재하는 색깔을 미리 찾습니다. (이 전처리 또한 O(NC)만큼의 시간 복잡도를 필요로 한다는 점에 유의하시기 바랍니다.) 이러한 소구간을 보통 버킷이라고 부릅니다. 전처리 후, 각 사진에는 최대 N/B개의 버킷이 포함되어 있습니다. 양 끝에 잘린 구간에는 각각 최대 B개의 불꽃이 포함될 수 있으므로, 양 끝의 소구간에서 절반보다 많은 색깔을 구하면, 미리 계산해 놓은 소구간들까지 색깔의 후보는 최대 N/B개입니다. 따라서, 각 사진마다 O(B + N/B)의 시간 복잡도가 소요됩니다. 전체 시간 복잡도를 구하면, 누적 합, 소구간 계산 등 전처리를 제외하고 O(M(B + N/B))가 됩니다.
위 식을 보면, B=N^0.5 일때 B와 N/B가 비슷해져 가장 효율적인 시간 복잡도를 얻을 수 있습니다. B=N^0.5인 경우 (즉, 각 버킷의 크기를 N^0.5 정도로 할 때) 시간 복잡도는 전처리를 제외하고 O(MN^0.5)입니다. 그러나, 전처리 과정이 여전히 O(NC)의 시간 복잡도를 요구합니다.
전처리 시간 줄이기
버킷을 활용한 풀이에서 전처리 과정이 NC만큼의 연산량을 요구하는 이유는, 크기가 B인 각 버킷에서도 사실상 C개의 색깔에 대해 몇 개의 불꽃이 그 색을 가지고 있는지 검사해 보아야 하기 때문입니다. 즉, 불꽃들의 수가 N에서 B로 줄어든 작은 문제를 푸는 것과 동일합니다.
그렇다면, 전체 문제를 쪼개 전처리를 통해 효율적으로 문제를 푸는 논리를 작은 문제들에 대해서도 적용할 수 있지 않을까요? (분할 정복의 적용입니다.) 전체 구간을 계속해서 절반으로 잘라 다음 그림과 같은 구조를 만들어 보도록 하겠습니다.
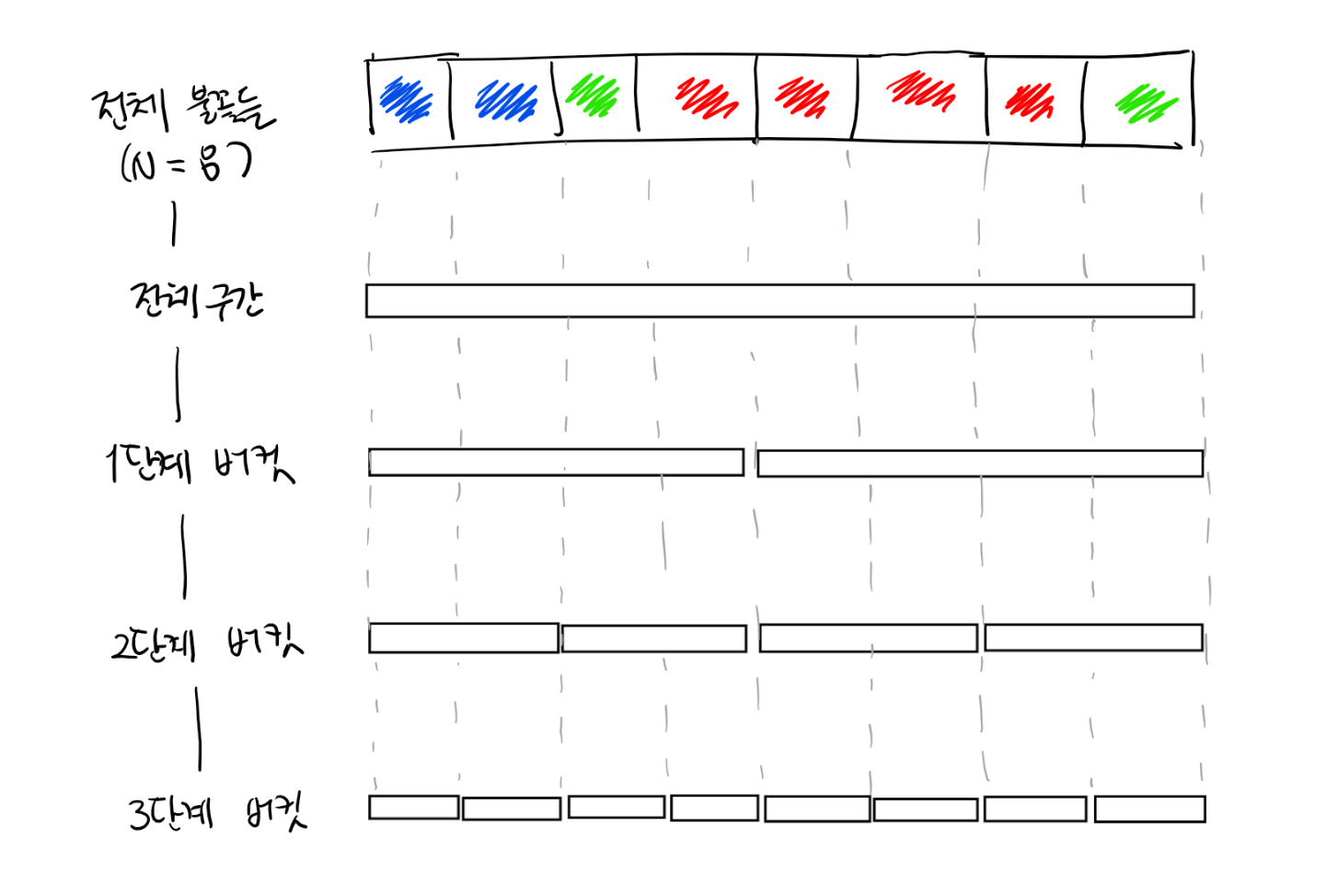
맨 위의 전체 구간은 모든 불꽃들을 포함하고 있는 버킷입니다. 이 구간을 절반으로 쪼갠 1단계 버킷들은 4개씩의 불꽃을 포함하고 있습니다. 계속해서 쪼개 나가면, 3단계 버킷은 불꽃이 하나씩 속해 있는 소구간이 됩니다.
이제 맨 아래의 가장 작은 버킷들부터 가장 많은 색깔을 계산해 나가도록 합시다. 3단계 버킷에서 ‘절반보다 많은 색깔’은 매우 쉽게 알 수 있습니다. 불꽃이 하나밖에 없기 때문에 당연히 그 색깔이 절반보다 많습니다.

여기에서 한 칸 위로 올라간 2단계 버킷은 각각 2개씩의 3단계 버킷을 포함하고 있습니다. 앞서 “전체 구간에서 절반보다 많이 존재하는 색깔은, 나눠진 구간 중 적어도 하나에서 절반보다 많이 존재하는 색깔이어야 한다.” 라고 했으니, 2단계 버킷에서 절반보다 많이 차지하는 색깔이 존재한다면, 버킷에 속한 2개의 3단계 버킷의 색깔 중 하나여야 합니다. 즉, 색깔의 후보가 2개밖에 없습니다. 각 2단계 버킷에서, 후보 색 2개에 대해 버킷 내에 그 색깔의 불꽃이 몇 개 있는지 계산하여 최종적인 결과를 계산합니다.
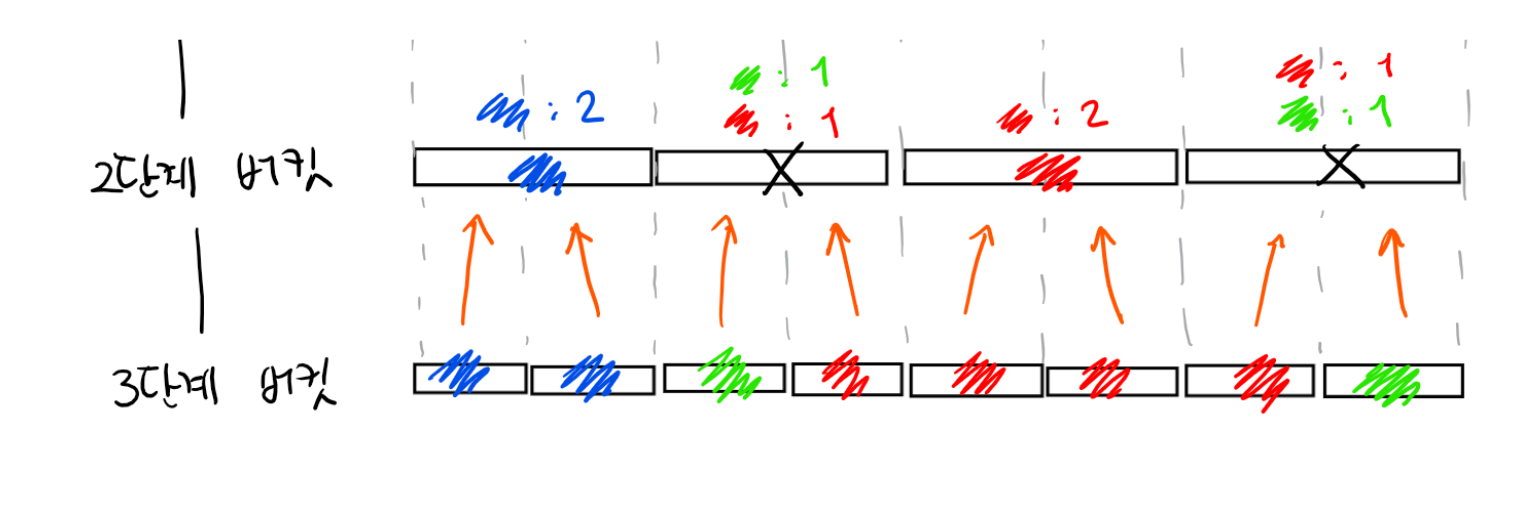
마찬가지로, 계속해서 위로 올라가면서 같은 방법으로 버킷의 색깔을 결정합니다.
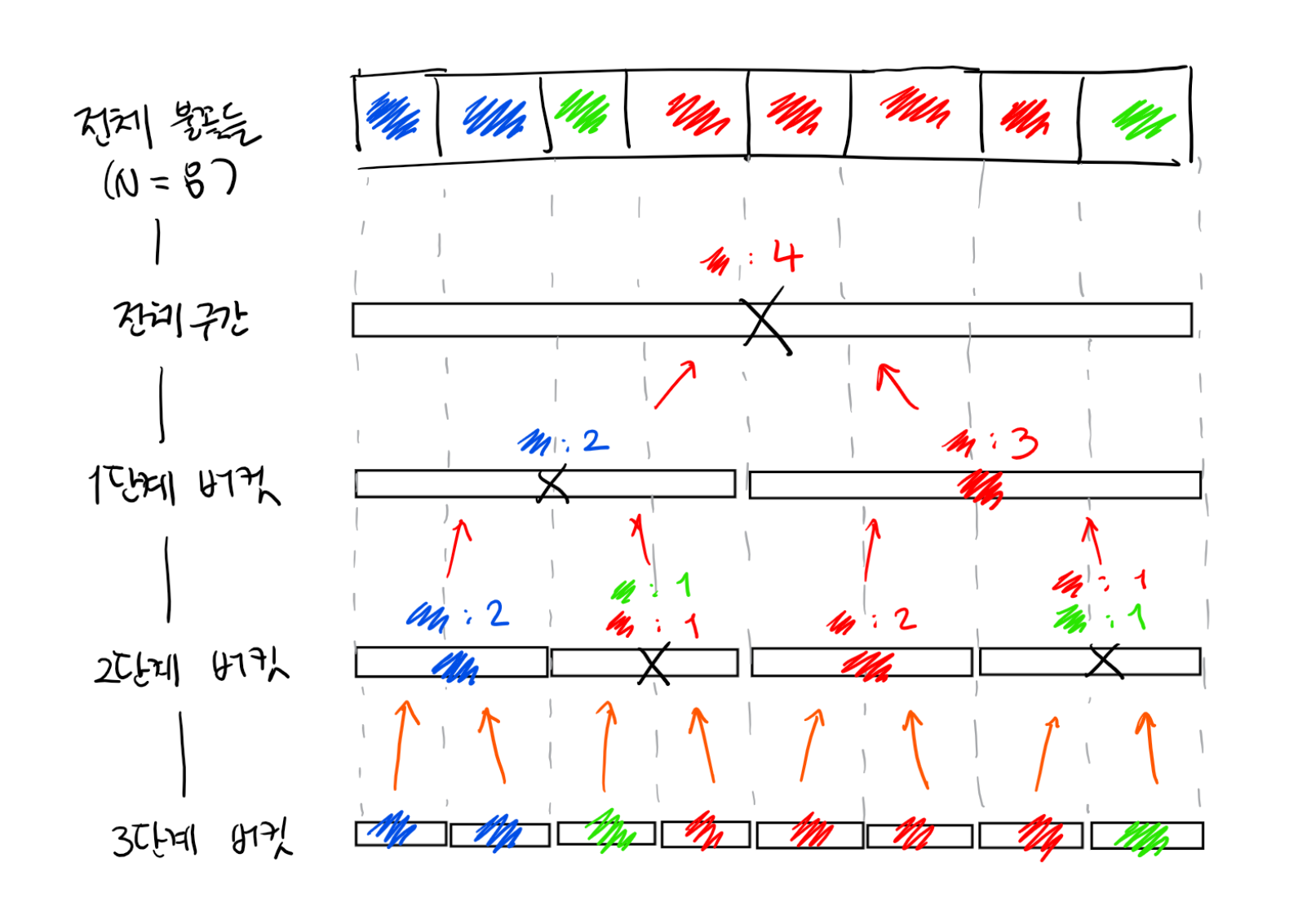
이러한 구조를 구간 트리(segment tree)라고 부르며, 이제부터 각 단계에 속한 버킷을 구간(segment)라고 부르기로 하겠습니다. 각 단계에서 구간의 개수는 1, 2, 4, 8, … 형태로 증가합니다. 전체 구간의 길이가 N일 때, 모든 단계에서 구간의 개수의 합은 2N을 넘지 않음을 관찰할 수 있습니다. 각 구간에서 아래 단계 구간 2개를 포함하고 있기 때문에 구간의 색깔을 결정하는 것은 2개의 색깔을 보는 것으로 충분합니다. 따라서, 구간 트리를 만드는 데 필요한 시간 복잡도는 O(N)입니다.
이제 구간 트리에서 사진에 대한 처리를 어떻게 하는지 알아봅시다. 앞선 버킷 풀이에서는 버킷의 크기가 모두 같았기 때문에 어떤 버킷을 써야 할지 쉽게 알 수 있었으나, 구간 트리는 구간들의 크기가 다양하기 때문에 약간의 고민이 필요합니다. 사용할 수 있는 가장 큰 구간을 사용한다라는 원칙을 정하면 고려해야 하는 구간들의 갯수를 최소한으로 할 수 있습니다.
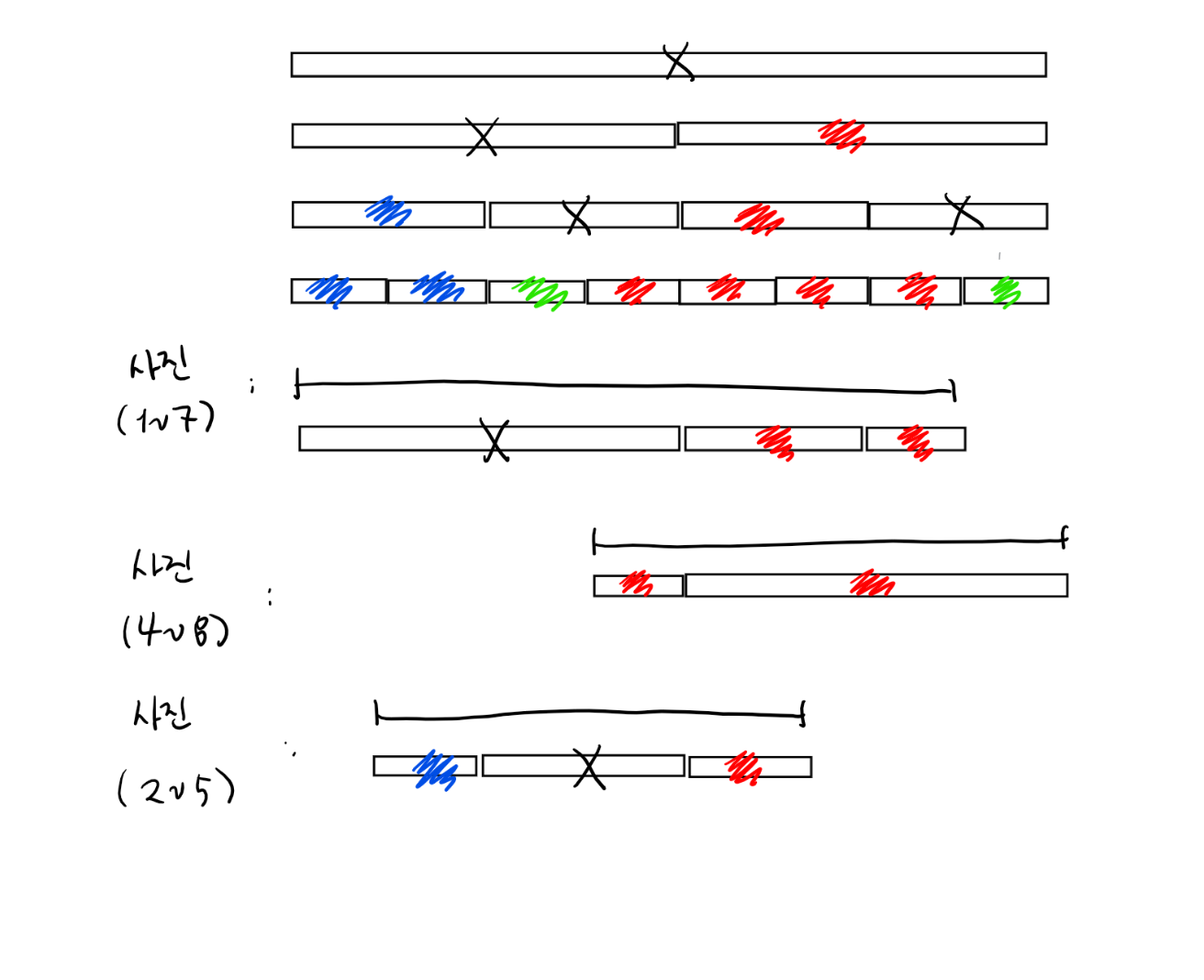
위 그림처럼, 다양한 단계의 구간을 활용하여 사진의 범위를 덮는 전략을 취하면 됩니다. 구간 트리는 임의의 사진의 범위에 포함되는 구간이 최대 2 logN개라는 성질을 가지고 있습니다. 따라서, 어떠한 사진이 질의로 주어지더라도 고려해야 하는 색깔 후보는 최대 2 logN개입니다. 즉, 사진마다 O(log N)의 시간 복잡도로 절반보다 많은 색깔을 찾아낼 수 있습니다.
정리하면,
- 전처리: 누적 합 배열을 계산하고, 구간 트리를 만든다.
- 각 사진에 대해,
- 사진의 범위에 들어오는 구간들을 찾는다.
- 구간들의 (전처리를 통해 미리 계산한) 색깔을 후보로 두고, 실제로 그 색깔이 사진에서 절반보다 많이 차지하고 있는지 검사한다.
이 알고리즘에서, 마지막으로 사진의 범위에 들어오는 구간을 찾는 것을 쉽게 구현하는 방법에 대해 다뤄보도록 하겠습니다. 재귀적으로 다음과 같은 과정을 수행합니다.
- 현재 구간이 사진의 범위에 완전히 포함되면, 후보에 포함시킨다.
- 현재 구간이 사진의 범위와 겹치지 않으면, 무시한다.
- 둘 다 아닐 경우, 구간을 절반으로 쪼개고 양쪽 구간에 대해 다시 살펴본다 (재귀).
예를 들어, 위의 그림처럼 N=8인 구간 트리를 만들었고 사진의 범위가 [1, 7]이라고 합시다. 그렇다면 다음과 같은 과정으로 알고리즘이 진행됩니다.
- 현재 구간: 전체
[1, 8] - 현재 구간이 사진의 범위에 부분적으로 겹치므로 절반
[1, 4], [5, 8]으로 쪼개고 다시 반복한다.- 현재 구간:
[1, 4] - 현재 구간이 사진의 범위에 포함되므로 후보에 포함시킨다.
- 현재 구간:
[5, 8] - 현재 구간이 사진의 범위에 부분적으로 겹치므로 절반
[5, 6], [7, 8]으로 쪼개고 다시 반복한다.- 현재 구간:
[5, 6] - 현재 구간이 사진의 범위에 포함되므로 후보에 포함시킨다.
- 현재 구간:
[7, 8] - 현재 구간이 사진의 범위에 부분적으로 겹치므로 절반
[7, 7], [8, 8]으로 쪼개고 다시 반복한다.- 현재 구간:
[7, 7] - 현재 구간이 사진의 범위에 포함되므로 후보에 포함시킨다.
- 현재 구간:
[7, 8] - 현재 구간이 사진의 범위와 겹치지 않으므로 무시한다.
- 현재 구간:
- 현재 구간:
- 현재 구간:
따라서 사진의 범위인 [1, 7]에 포함되는 구간 [1, 4], [5, 6], [7, 7]을 올바르게 찾을 수 있습니다. 다른 두 개의 예시에 대해서도 직접 알고리즘이 진행되는 과정을 생각해 보시기 바랍니다.
구간 트리는 일렬로 나열된 데이터를 다루는 데 굉장히 유용한 자료 구조입니다. 강력한 성능을 가지고 있고 응용될 수 있는 부분이 많기 때문에 문제 해결 분야에서 실력을 키우기 위해서는 구간 트리에 대해 많은 공부가 필요합니다.
확률론적 풀이
다른 관점에서 이 문제의 풀이에 접근해 봅시다. 우리가 앞선 풀이에서 많은 시간 복잡도를 잡아먹는 이유는, 어떤 구간에서 절반 이상을 차지할 수 있는 색깔의 후보가 최대 C개이기 때문에, 일일이 C개의 색깔을 확인해야 하기 때문이었습니다. 그리고 뒤에 이 풀이를 개선한 풀이도 색깔의 후보를 줄여 시간 복잡도를 줄이는 전략을 취했습니다. 하지만, 실제로 색깔의 후보가 그렇게 많을까요?
s~e의 구간에 절반 넘게 차지하고 있는 색깔이 존재한다고 가정합시다. 우리가 s~e의 구간에서 ‘아무거나’ 불꽃 하나를 선택했을 때 그 불꽃이 절반 이상을 차지하는 색깔일 확률은 적어도 1/2입니다. 만약 불꽃을 아무거나 20개 고른다면, 그 중 적어도 하나가 그 색깔일 확률은 1 - (1/2)^20으로 매우 작습니다! 무작위로 택하는 불꽃의 갯수가 늘어날수록, 이 확률은 매우 급격하게 줄어듭니다. 따라서, 이러한 전략을 생각해 볼 수 있습니다.
- 각 구간
(s, e)에 대해서,- s~e 중에 있는 불꽃 중 아무거나 하나를 고릅니다.
- 그 불꽃의 색깔이 이 구간에 몇 개 있는지 셉니다.
- 만약 그 색깔이 절반보다 많다면, 단조로운 사진으로 판단합니다.
- 1-3을 적당한 횟수, p번만큼 반복합니다. p번 후에도 절반보다 많은 색깔을 찾을 수 없다면, 단조롭지 않은 사진으로 판단합니다.
이 전략에서 오답을 낼 확률은 얼마일까요? 일단, 단조롭지 않은 사진을 단조로운 사진으로 잘못 판단할 가능성은 존재하지 않습니다. 반대로, 단조로운 사진을 단조롭지 않은 사진으로 판단할 확률은 앞서 계산했듯이 (1/2)^p 입니다.
우리에게 M개의 질의가 주어지므로, M개의 질의를 전부 맞출 확률은 (1 - (1/2)^p)^M입니다. 이 확률이 95% 이상이려면 (즉, 95% 확률로 문제 전체에 대해 옳은 답을 내려면) p가 얼마 이상이어야 할까요? M=100일 경우 p의 최솟값은 10.9xxx로, 11번 이상 뽑으면 꽤 높은 확률로 100개의 질의에 올바르게 대답할 수 있게 됩니다. M=1000일 경우 p=15, M=10000일 경우 p=21입니다. 대략 M이 10배 증가할 때 p가 5씩 증가하는 것으로 보아, p는 M의 로그값에 비례한다고 생각할 수 있습니다. 위 알고리즘의 시간 복잡도는 (특정 색깔이 구간에 몇 개 있는지 전처리를 통해 O(1)에 알 수 있다면) 전처리를 제외하고 O(Mp), 즉 O(MlogM) 정도가 됩니다.
이와 같은 접근은 기존과 달리 모든 경우에 대해 항상 맞는 답을 기대할 수 없는 확률적인 접근이지만, 컴퓨터과학의 다양한 분야에 적용되고 있습니다. 가끔 정석적인 방법으로 쉬운 풀이를 찾을 수 없을 때 이러한 관점에서 생각하는 것도 많은 도움이 됩니다.
입력/출력 예제
입력 형식
- 첫 번째 줄에는 불꽃의 개수 N(3 <= N <= 300,000)과 색깔의 종류 C(1 <= N <= 10,000)이 공백으로 구분되어 입력된다.
- 두 번째 줄에는 각 불꽃의 색깔이 공백으로 구분되어 입력된다. 색깔은 1 이상 C 이하의 정수로 주어진다.
- 세 번째 줄에는 사진의 개수 M(1 <= M <= 10,000)이 주어진다.
- 다음 M개의 줄에는 사진에 나온 불꽃들의 정보가 두 개의 정수 A_i, B_i로 주어진다. 이는 i번째 사진에 A_i번째 불꽃부터 B_i번째 불꽃이 나왔음을 의미한다.
출력 형식
M개의 줄에 각 사진이 단조로운지, 단조롭지 않은지 판단하여 단조롭지 않다면 no를 출력하고, 단조롭다면 yes와 그 사진에서 절반보다 많이 차지하는 색깔을 출력한다.
입력 예제 1
10 3
1 2 1 2 1 2 3 3 2 3
4
1 2
2 4
6 9
7 10
출력 예제 1
no
yes 2
no
yes 3
원문
Snow White and the N dwarfs live in the forest. While the dwarfs mine away Snow White hangs around social networks.
Each morning the dwarfs form a long line and go whistling away to the mine. Snow White runs around them and snaps pictures to upload onto her favorite social network. When dwarfs enter the mine, Snow White goes back to their house and goes through the pictures, selecting pretty ones. Each dwarf has a colored cap, and there are C different colors. A picture is pretty if more than half caps on it are of the same color. In other words, if there are K dwarfs on the picture, it is pretty if strictly more than K / 2 dwarfs have same colored caps.
Write a program that will check for a set of M pictures if they are pretty, and what color is dominating if they are.
출처
Croatian Open Competition in Informatics 2009/2010, Contest 3, #5 (PATULJCI)