화물열차 (cargo-trains)
2019.04.26문제
이웃한 레일 위에 놓인 두 화물 열차 사이에 짐을 옮기려고 한다. 화물 열차는 다양한 길이를 가지 컨테이너가 여러 개 연결된 형태인데, 컨테이너가 놓인 칸이 가장 많이 겹치도록 두 화물 열차를 겹쳐 놓으면 짐을 옮기는 과정이 수월하다. 처음에 두 화물 열차는 아래 그림과 같이 첫 칸의 앞부분이 서로 마주보며 같은 선에 위치하고 있다. 화물 열차 A는 가만히 있고, 화물 열차 B를 움직여 컨테이너가 놓인 칸이 가능한 많이 겹쳐지게 하려고 한다.
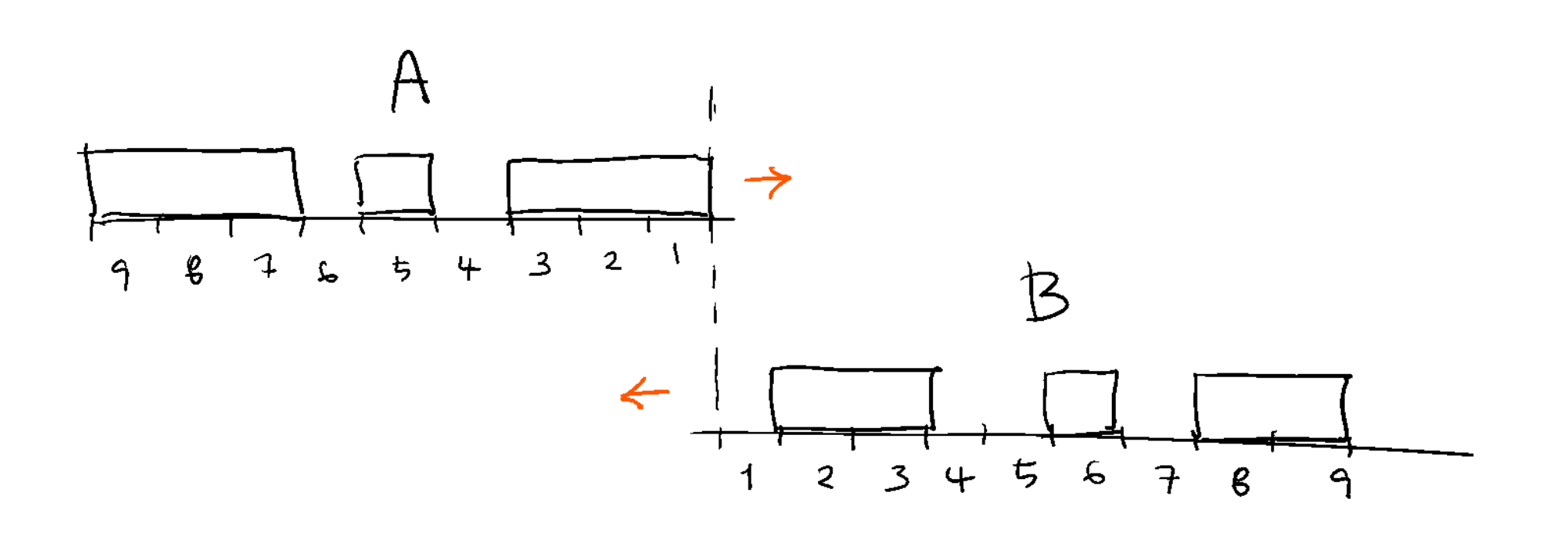
- 화물 열차 A는 컨테이너 N개가 연결된 열차이고, 화물 열차 B는 컨테이너 M개가 연결된 열차이다.
- 화물 열차의 최대 길이는 L이다.
예시
각 컨테이너의 위치를 구간으로 나타내자. 즉, 문제에서 제시한 그림의 경우 다음과 같이 표현할 수 있다.
A: [1, 3], [5, 5], [7, 9] (N=3)B: [2, 3], [6, 6], [8, 9] (M=3)
이 경우, 열차 B를 앞으로 10칸 옮기면 다음과 같이 5칸을 겹칠 수 있으며, 이것이 최대이다.
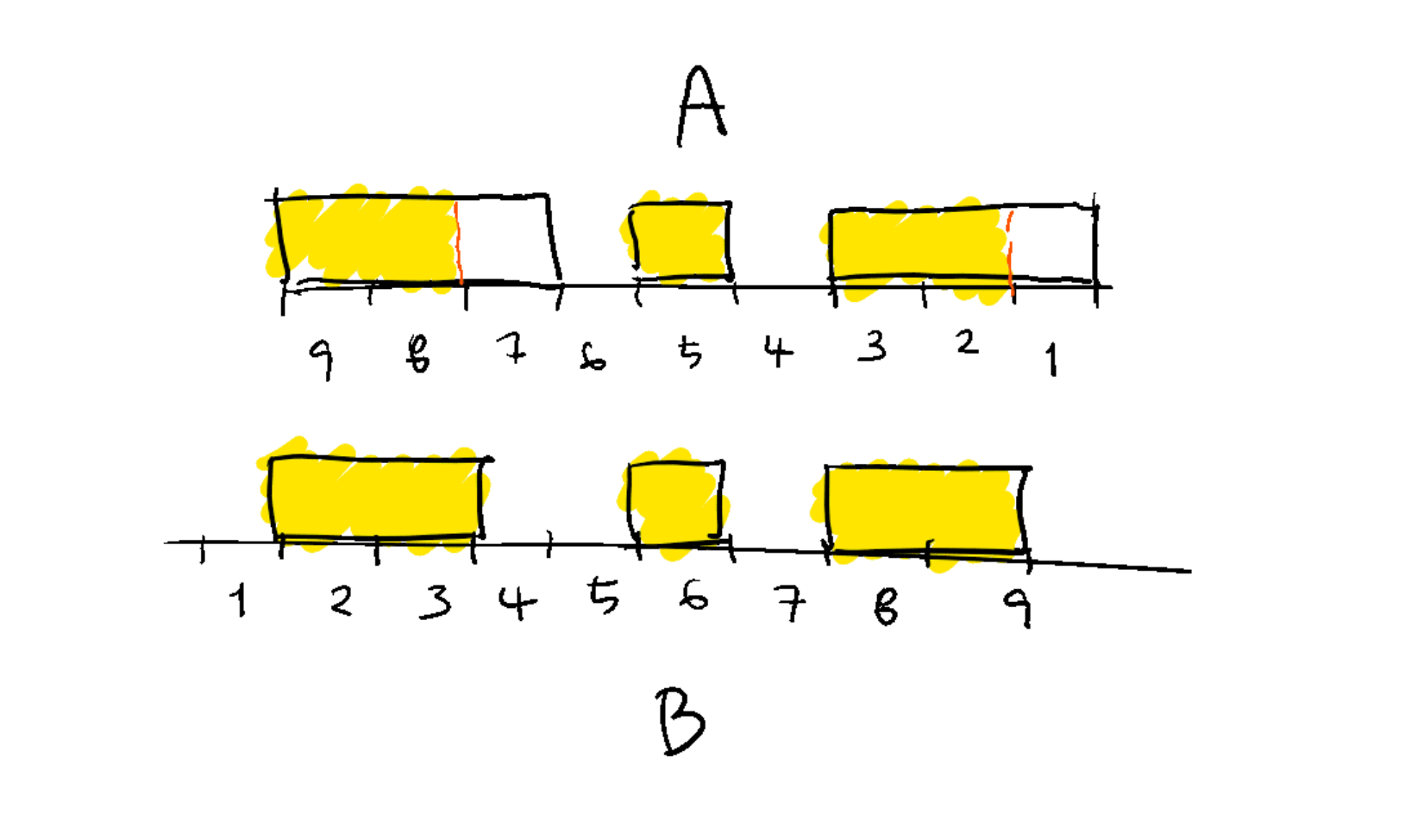
관찰
먼저, 서술의 편의를 위해 열차 A와 B의 칸 번호를 다음과 같이 다시 붙여 서로 공유하도록 하겠습니다. 실제로 프로그래밍을 할 때는 적절한 전처리를 통해 컨테이너 구간의 번호를 다시 붙여 주면 됩니다.
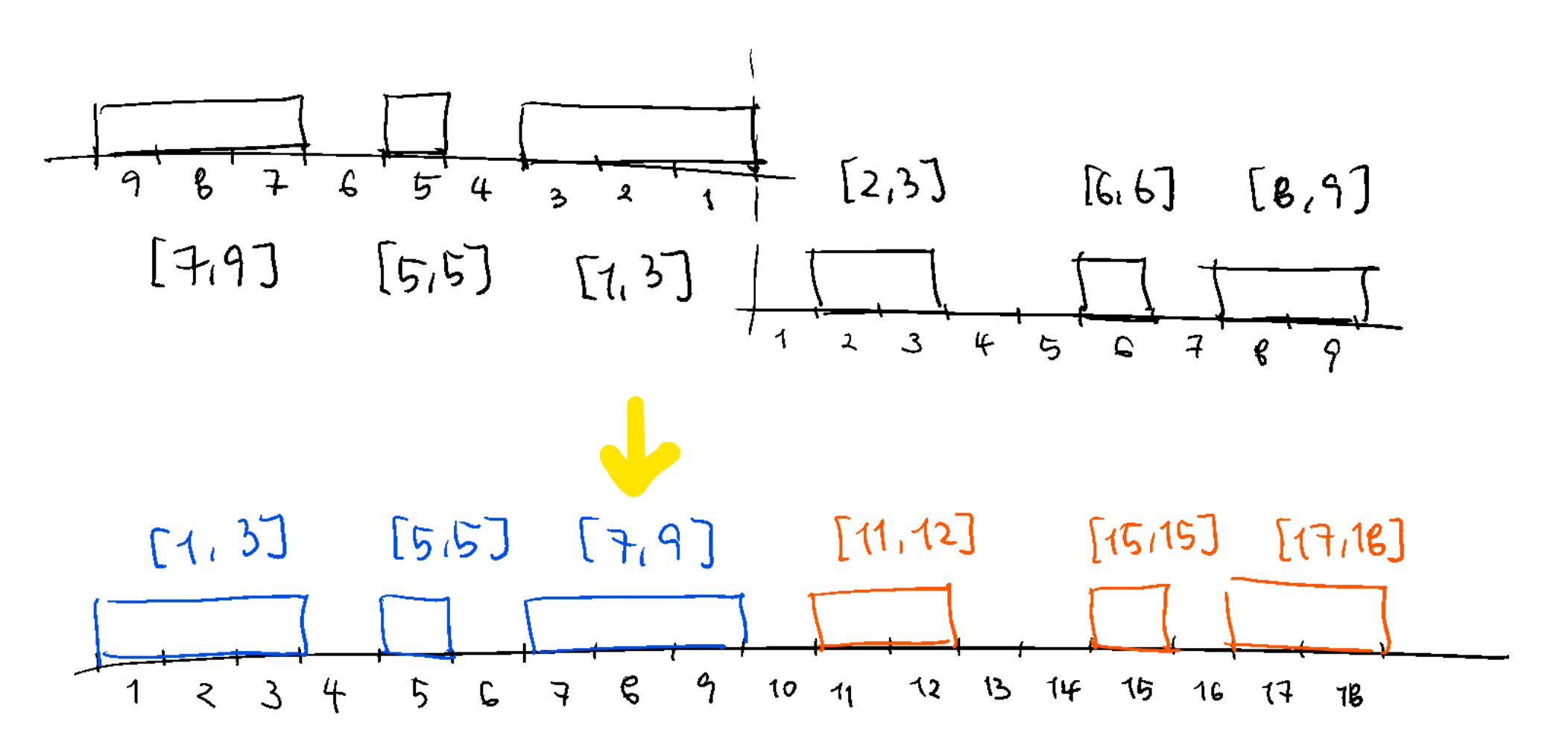
당연하게도, 가장 먼저 떠오르는 알고리즘은 열차 B를 한 칸씩 옮겨 보면서, 그때마다 몇 개의 칸이 겹치는지 세어 최적의 경우를 찾는 것입니다. 열차 B를 옮겼을 때, 겹치는 칸의 개수는 어떻게 셀 수 있을까요?
- 모든 칸을 일일이 확인하면서, 두 열차에 대해 그 칸에 컨테이너가 있는지 확인하는 방법을 적용할 수 있습니다. 이 경우, 열차의 길이만큼의 칸들을 확인해야 겹치는 칸의 개수를 알 수 있습니다. 따라서, 열차 B를 옮길 때마다
O(L)의 시간 복잡도가 소요됩니다. - 열차 B를 옮길 수 있는 경우의 수는, 겹치는 칸이 없는 처음 상태(0칸)부터 열차 B를 앞으로 (열차 A의 길이) + (열차 B의 길이) 만큼 진행시켜 다시 겹치는 칸이 없는 상태까지 고려해야 합니다. 따라서, 최대 2L-1가지 가능성을 고려해야 합니다. 따라서, 전체 시간 복잡도는
O(L^2)가 됩니다.
다만, 컨테이너에 속한 칸이 [1, 3], [7, 9]와 같이 연속한 구간으로 존재한다는 점을 이용할 수 있습니다. 만약 열차 A의 어떤 컨테이너가 [1, 6]의 구간에 있고, 열차 B를 옮겼을 때 열차 B의 어떤 컨테이너가 [3, 9] 구간에 존재한다면, 우리는 1~9번 칸을 일일이 확인하지 않아도 두 구간이 겹치는 구간이 [3, 6]이라는 사실을 쉽게 알 수 있습니다. 이 생각을 일반화하면,
- 열차 A의 컨테이너가
[s1, e1]구간에 존재하고, 열차 B의 컨테이너가[s2, e2]구간에 존재한다면, 두 컨테이너가 겹치는 칸의 개수는 다음과 같습니다.e1 < s2이거나s1 > e2일 경우, 서로 겹치지 않는다. (0칸)- 이외의 경우,
min{e1, e2} - max{s1, s2} + 1칸 겹친다.
또한, 열차 B를 앞으로 k칸 옮길 경우, 원래 열차 B의 컨테이너 [s, e]는 [s - k, e - k]로 이동하게 된다는 성질도 관찰할 수 있습니다. 이 두 가지 성질을 이용하면, 모든 칸을 확인하는 대신 모든 컨테이너를 확인하는 것으로 기존의 알고리즘을 대체할 수 있습니다.
- 열차 A의 컨테이너와 열차 B의 컨테이너 쌍에 대해, 두 컨테이너의 겹치는 칸 개수를 확인하는 것은
O(1)에 수행할 수 있습니다. 쌍의 개수가 총 NM개이므로, 열차 B를 옮길 때마다O(NM)의 시간 복잡도가 소요됩니다. 따라서, 전체 시간 복잡도는O(LMN)입니다.
풀이
그래프를 통한 접근
그러나, 여전히 열차 B를 한 칸씩 옮겨 보아야 한다는 점이 마음에 걸립니다. 이 과정을 더 최적화 할 수 있는 방법은 없을까요?
다음 그림은 열차 A의 컨테이너와 열차 B의 컨테이너가 서로 반대쪽에서 접근할 때 부터 서로 지나쳐 완전히 멀어질 때까지 서로 겹치는 칸 개수를 나타낸 그래프입니다.
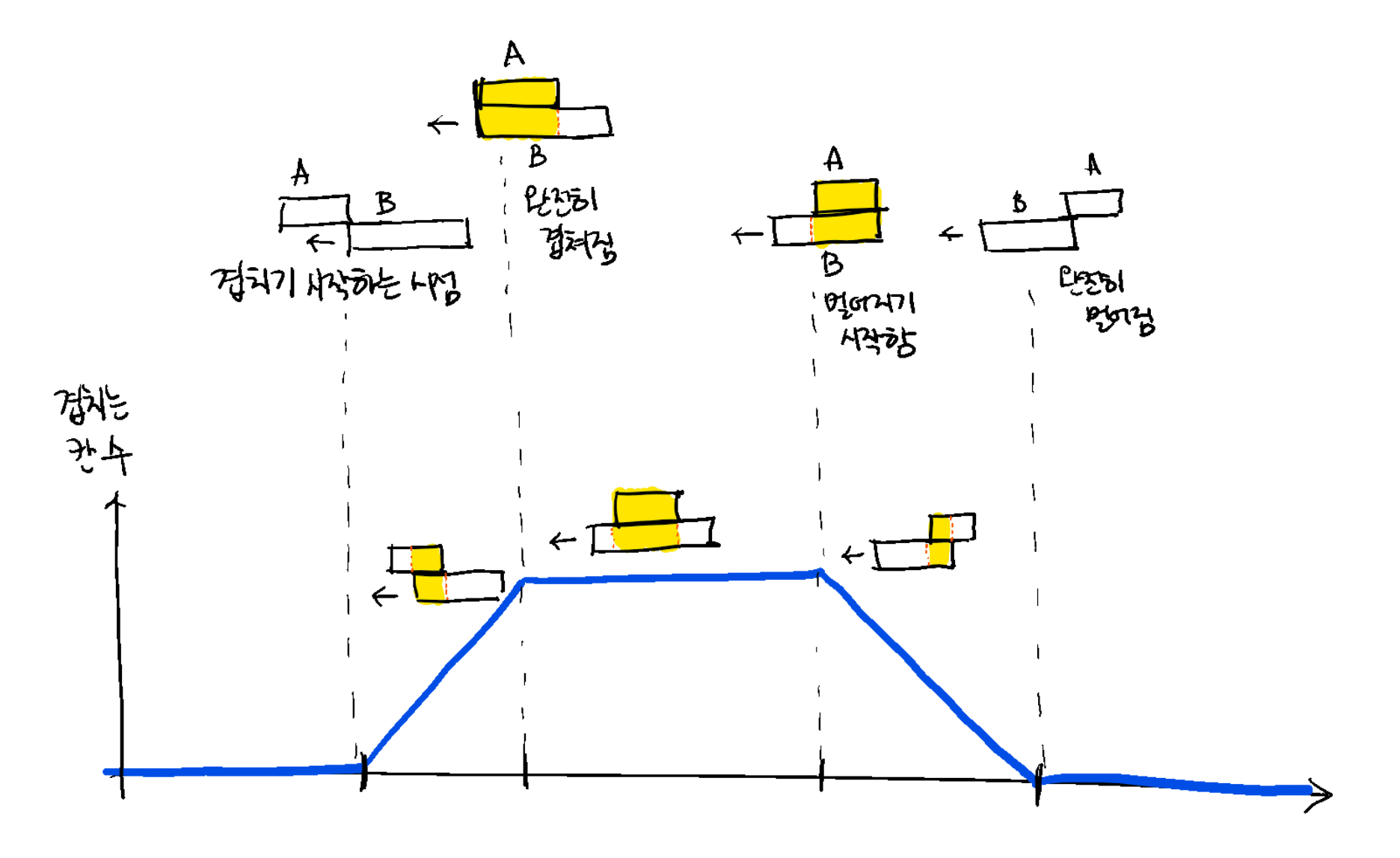
두 컨테이너의 길이가 어떻게 주어지더라도, 위 그래프와 같이 사다리꼴 (또는 삼각형) 모양의 그래프가 나타난다는 점이 이 문제의 풀이에 접근하는 핵심입니다.
열차 A의 컨테이너 구간 위치가 [s1, e1]이고, 열차 B의 처음 컨테이너 구간 위치가 [s2, e2]라고 합시다. 이로부터 다음과 같은 성질을 알 수 있습니다. (직접 증명해 보시기 바랍니다.)
- 처음에는 열차 B가 A보다 완전히 오른쪽에 있으므로,
s1 <= e1 < s2 <= e2임이 보장된다. - 두 컨테이너가 겹치기 시작하는 시점은 열차 B가
s2 - e1칸 앞으로 이동했을 때이다. - 두 컨테이너가 최초로 완전히 겹쳐진 시점은 두 컨테이너의 길이에 따라 경우가 나눠지는데, A의 컨테이너가 더 긴 경우에는
e2 - s2이고, B의 컨테이너가 더 긴 경우에는e1 - s1이다. - 두 컨테이너가 마지막으로 완전히 겹쳐진 시점은, 반대로 A의 컨테이너가 더 간 경우에
e1 - s1이고 B의 컨테이너가 더 긴 경우에e2 - s2이다. - 두 컨테이너가 마지막으로 겹친 시점은
e2 - s1이다. - 사다리꼴 모양 그래프에서 평평한 부분의 높이는 두 컨테이너의 길이 중 작은 값이다.
열차 A의 컨테이너와 B의 컨테이너 하나에 대해서만 생각하면, 열차 B가 앞으로 진행할 때 이러한 그래프가 그려집니다. 만약 열차 A에 컨테이너가 총 2개 있고, B에는 1개만 있다면 (컨테이너 A-1, 컨테이너 B-1)와 (컨테이너 A-2, 컨테이너 B-1)의 조합을 독립적으로 생각하여 이 그래프를 두 개 그릴 수 있습니다. 다음 그림을 보면서 이해해 봅시다.
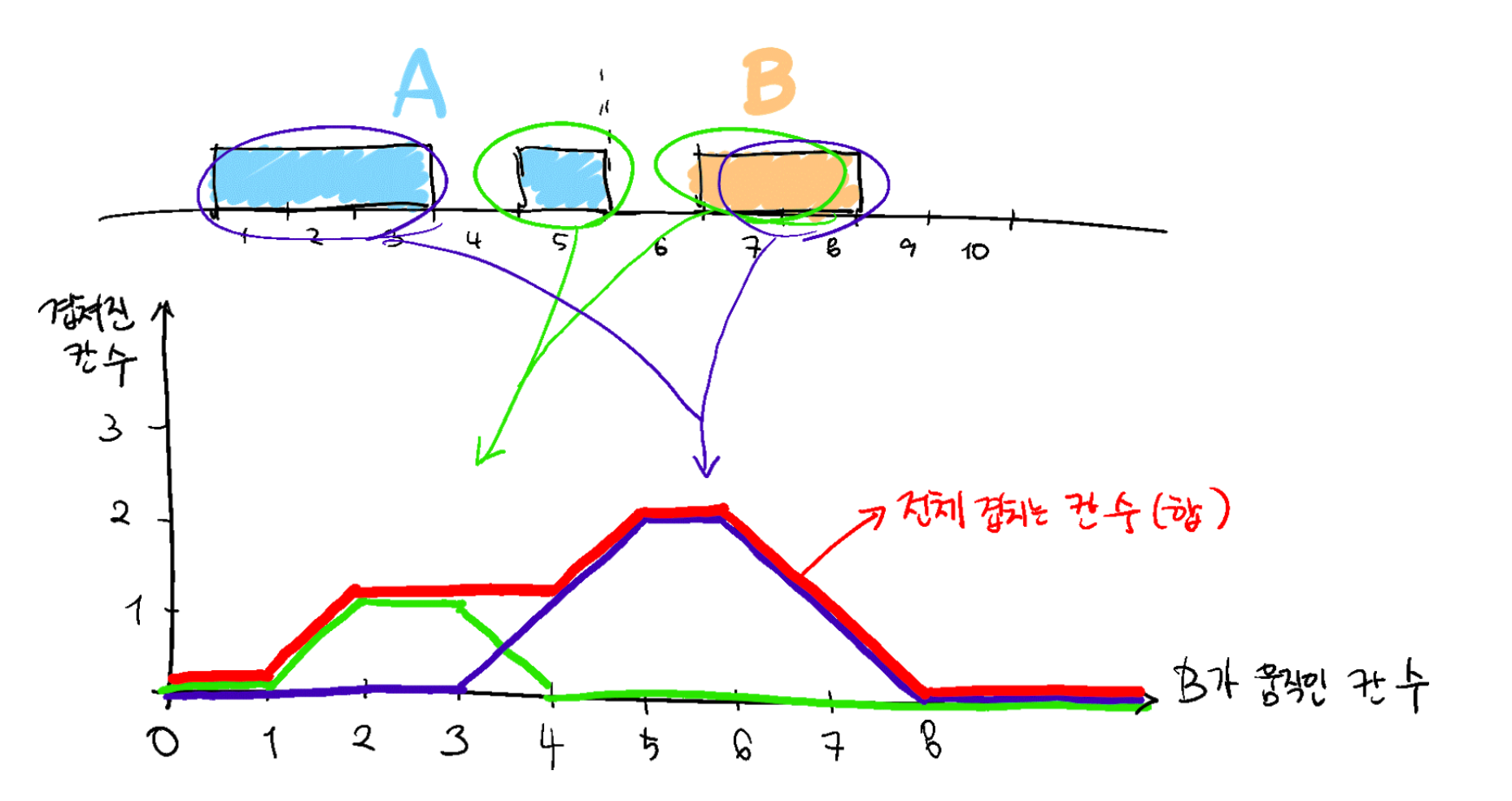
연두색 그래프는 (컨테이너 A-1, 컨테이너 B-1)에 대해 겹치는 칸 개수의 변화를 그린 것이고, 보라색 그래프는 (컨테이너 A-2, 컨테이너 B-1)에 대해 겹치는 칸 개수의 변화를 그린 것입니다. 빨간색 그래프는 두 그래프의 합, 즉 두 열차 전체가 겹치는 칸 개수의 변화를 나타내고 있습니다. 이러한 생각을 확장하면, 컨테이너가 N개 있는 열차 A와 컨테이너가 M개 있는 열차 B의 상황은 NM개 사다리꼴 모양 그래프의 합으로 나타낼 수 있습니다.
그래프를 축약하여 나타내기
사다리꼴 모양의 그래프는 단 4개의 데이터만으로 축약할 수 있습니다.
- 최초로 두 컨테이너가 겹친 시점
- 최초로 완전히 겹친 시점
- 마지막으로 완전히 겹친 시점
- 마지막으로 두 컨테이너가 겹친 시점
예를 들어, 앞서 그려 보았던 (컨테이너 A-1, 컨테이너 B-1)의 그래프는 (1, 2, 3, 4)로, (컨테이너 A-2, 컨테이너 B-1)의 그래프는 (3, 5, 6, 8)로 축약할 수 있습니다. 이 네 개의 숫자만으로도 임의의 시점에서 그래프의 값이 무엇인지 알 수 있다는 점에 주목하시기 바랍니다.
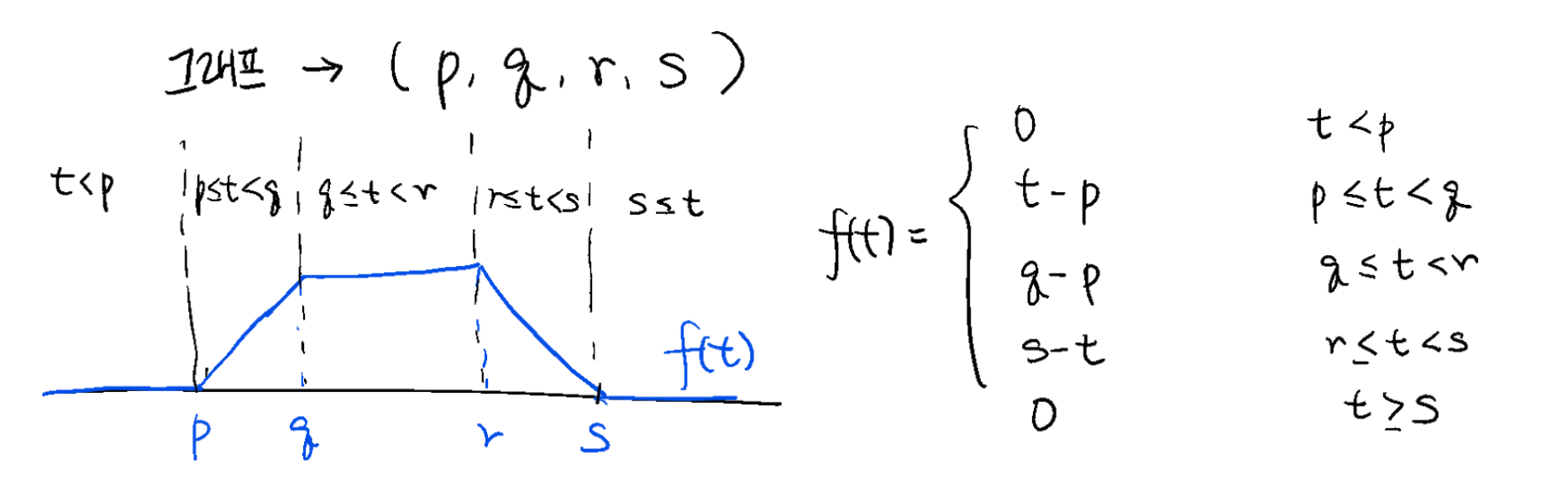
이를 확장하여 전체 열차에 대한 그래프처럼 좀 더 복잡한 모양의 그래프를 축약하여 나타낼 수 있는 방법에 대해 생각해 봅시다.
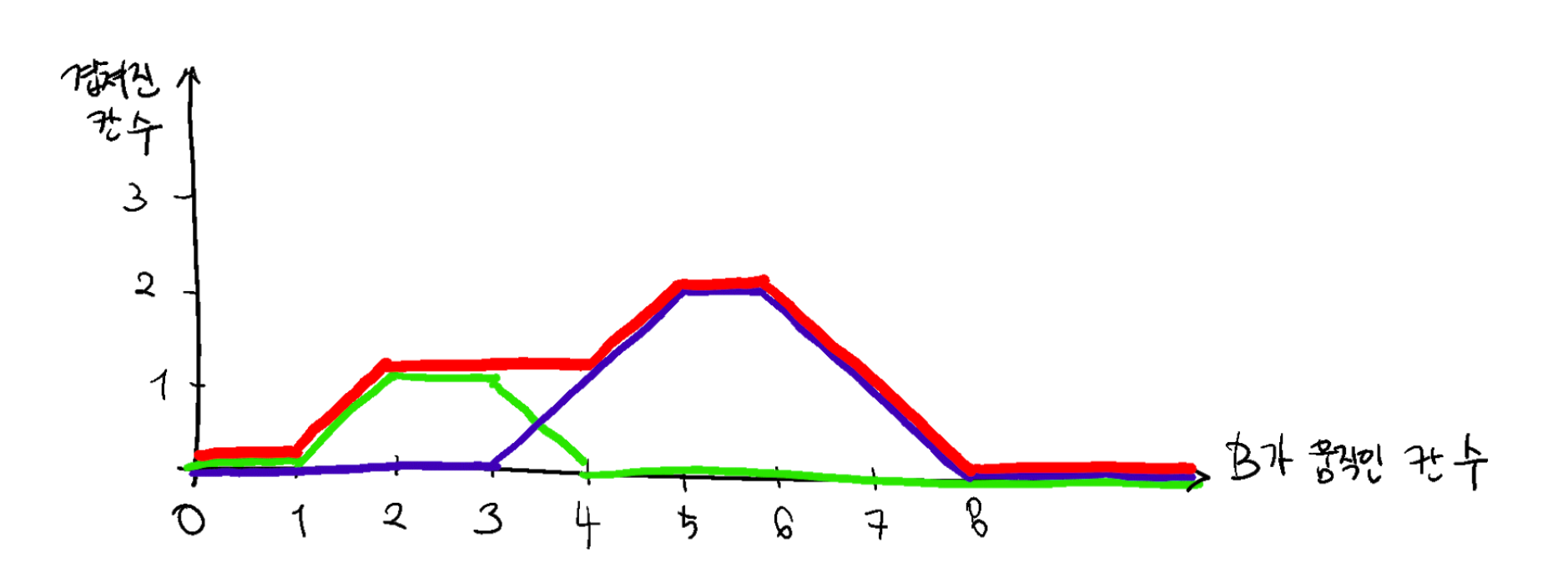
빨간색 그래프는 수직선 전체에 대해 값을 가지고 있지만, 그 값은 규칙적으로 변합니다. 특별한 변화가 일어나는 지점은 그래프가 꺾이는 지점 (t = 1, 2, 4, 5, 6, 8) 뿐입니다. 따라서, 앞서 사다리꼴 모양 그래프에서 했던 것처럼 그래프가 꺾이는 지점의 정보만으로 그래프를 요약할 수 있습니다. 꺾이는 지점에서는 그 위치(t)와 기울기의 변화(s)로 꺾이는지를 저장하면 됩니다.
[(t=1, s=1), (t=2, s=-1), (t=4, s=1), (t=5, s=-1), (t=6, s=-1), (t=8, s=1)]
두 그래프의 합을 구하는 것도 간단하게 할 수 있습니다. 위의 예시에서 연두색 그래프와 보라색 그래프를 요약하면 다음과 같습니다.
- 연두색:
[(t=1, s=1), (t=2, s=-1), (t=3, s=-1), (t=4, s=1)] - 보라색:
[(t=3, s=1), (t=5, s=-1), (t=6, s=-1), (t=8, s=1)]
이제 t가 작은 순서대로 채워 나가는데, t가 같은 것이 여러 개 있는 경우에는 기울기의 변화를 모두 합하여 저장합니다. (변화가 0인 경우에는 지워줍니다.) 더 구체적으로는, 두 그래프에 속한 데이터들을 단순히 같이 넣고 재정렬하여 합한 그래프를 만들 수 있습니다. 이 경우, 데이터 개수를 k라고 할 때 정렬 때문에 O(k log k)의 시간 복잡도가 필요합니다. 그러나, 슬라이딩 윈도우 방법을 활용하면 O(k)의 시간 복잡도에 그래프를 합할 수 있습니다.
합(빨간색):
[(t=1, s=1), (t=2, s=-1), (t=3, s=1+(-1)=0), (t=4, s=1), (t=5, s=-1), (t=6, s=-1), (t=8, s=1)]
문제에서는 겹치는 칸의 최대값과 최대값으로 만드는 시점이 무엇인지를 요구하므로, 이러한 그래프에서 최대값을 어떻게 찾을 수 있는지 생각해 봅시다. 맨 왼쪽부터 기울기와 그래프의 값을 계속 계산해 나가면 됩니다. (기울기의 변화값으로부터 기울기와 원래 함수값을 ‘적분’한다는 개념으로도 생각할 수 있습니다.) 예시로 든 그래프를 통해 알아봅시다.
| 시점 | 기울기 변화값 | 기울기 | 실제 값 (겹치는 칸 수) |
|---|---|---|---|
| 처음 (t < 1) | - | 0 | 0 |
| t = 1 | 1 | 0 + 1 = 1 | 0 |
| t = 2 | -1 | 1 + (-1) = 0 | 0 + 1 * (2 - 1) = 1 |
| t = 4 | 1 | 0 + 1 = 1 | 1 + 0 * (4 - 2) = 1 |
| t = 5 | -1 | 1 + (-1) = 0 | 1 + 1 * (5 - 4) = 2 |
| t = 6 | -1 | 0 + (-1) = -1 | 2 + 0 * (6 - 5) = 2 |
| t = 8 | 1 | (-1) + 1 = 0 | 2 + (-1) * (8 - 6) = 0 |
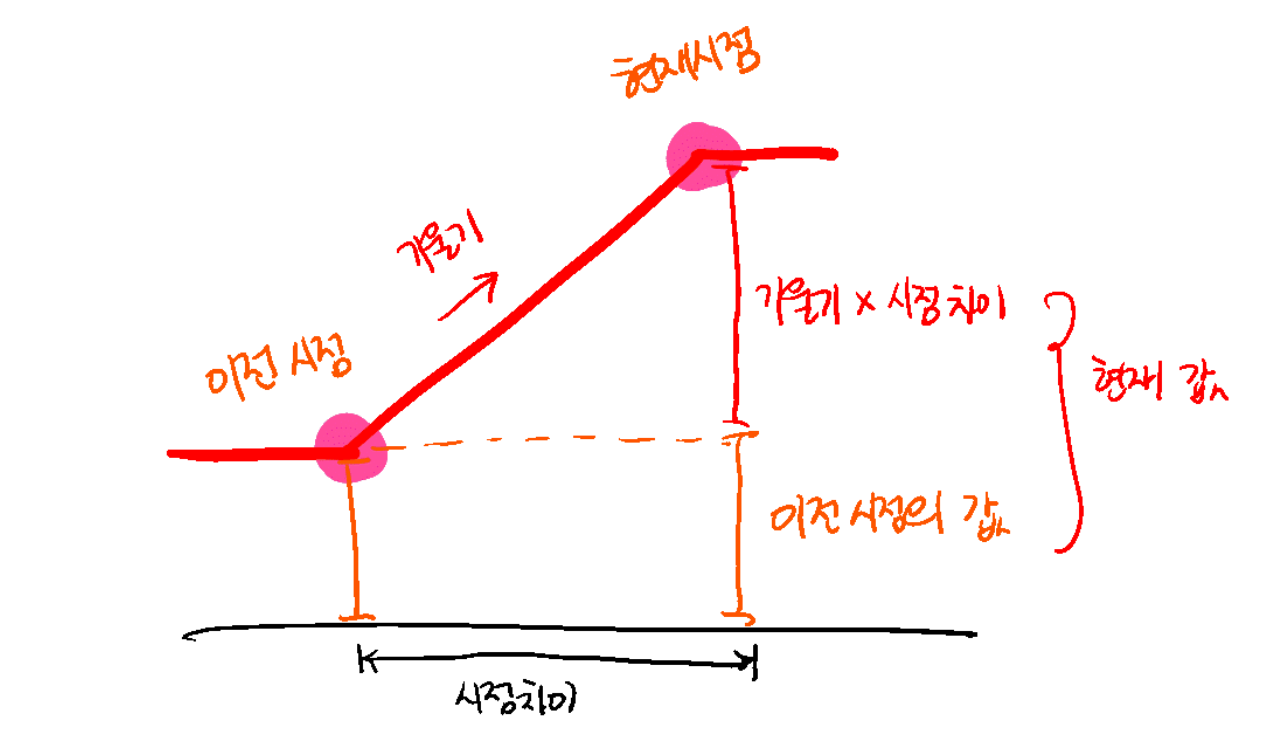
위의 그림에서 빨간색 그래프의 실제 값과 이 방법으로 통해 구한 값이 같음을 서로 비교해 보도록 하시기 바랍니다. 그래프의 값을 계속 구해 나가면서 최대값을 찾으면 예시 그래프의 경우 최대값이 2라는 것을 알아낼 수 있습니다.
이 알고리즘의 시간 복잡도는 요약한 그래프에 꺾이는 지점이 총 몇 개인지에 따라 달라집니다. 왜냐하면, 두 그래프를 합하는 것도 꺾이는 지점의 개수만큼의 시간 복잡도가 소요되고, 마지막에 최대값과 그 시점을 구하는 것 또한 그만큼의 시간 복잡도가 소요되기 때문입니다. 사다리꼴 모양의 그래프는 4개의 꺾이는 지점을 가지고 있습니다. 합해야 하는 그래프가 총 NM개이므로, 이 그래프를 모두 합해도 최종적인 그래프의 꺾이는 지점은 4NM개를 넘지 않습니다. 따라서, 이 알고리즘의 시간 복잡도는 O(NM)입니다. 열차의 길이 L에 시간복잡도가 무관하다는 점에 유의하시기 바랍니다.
정리하면, 다음과 같은 알고리즘으로 이 문제를 풀 수 있습니다.
- 열차 A의 컨테이너와 열차 B의 컨테이너 쌍들에 대해, NM개의 사다리꼴 그래프를 만든다. 그래프를 만들 때는 요약한 형태로 만들어 관리한다.
- NM개의 사다리꼴 그래프를 합하여 전체 그래프를 만든다.
- 전체 그래프를 따라가며 최대값과 최대값이 등장하는 시점을 구한다.
입력/출력 예제
입력 형식
- 첫 번째 줄에는 열차 A의 컨테이너 개수 N이 주어진다. (1 <= N <= 1,000)
- 이어 N개의 줄에는 각 컨테이너의 구간 [S, E]가 앞에서부터 순서대로 주어진다. (1 <= S <= E <= 10^9)
- N+2번째 줄에는 열차 B의 컨테이너 개수 M이 주어진다. (1 <= M <= 1,000)
- 이어 M개의 줄에는 마찬가지로 각 컨테이너의 구간 [S, E]가 앞에서부터 순서대로 주어진다. (1 <= S <= E <= 10^9)
출력 형식
컨테이너가 놓인 칸을 최대로 겹쳐지게 하기 위해 열차 B를 앞으로 몇 칸 움직여야 하는지 출력한다. 만약 최대로 겹쳐지게 하는 경우가 여러 가지라면, 그 중 최솟값을 출력한다.
입력 예제 1
3
1 3
5 5
7 9
3
2 3
6 6
8 9
출력 예제 1
10
원문
이웃한 레일 위에 놓인 두 화물 열차 사이에 짐을 옮기려고 한다. 화물 열차의 각 칸에는 컨테이너가 놓여 있기도 하고, 놓여 있지 않기도 한데 컨테이너가 놓인 칸이 가장 많이 겹치도록 두 화물 열차를 겹쳐 놓으면 짐을 옮기는 과정이 수월하다. 처음에 두 화물 열차는 아래 그림과 같이 첫 칸의 앞부분이 서로 마주보며 같은 선에 위치하고 있다. 화물 열차 A는 가만히 있고, 화물 열차 B를 움직여 컨테이너가 놓인 칸이 가능한 많이 겹쳐지게 하려고 한다. 화물 열차 B를 몇 칸 앞으로 움직여야 하는지 구하는 프로그램을 작성하시오.
출처
한국정보올림피아드 지역본선, 2005년, 고등부 4번 (화물 열차)