Union-Find 자료구조
2019.04.25Union-Find 자료구조는 많은 원소가 여러 개의 서로소 집합(서로 겹치지 않는 집합)으로 나누어진 상태를 표현하기 위한 자료구조입니다.
예시로, 1~8까지 8개의 원소가 3개의 집합 {1, 2, 5}, {3, 6}, {4, 7, 8}로 나누어져 있다고 생각해 봅시다. Union-Find 자료구조에서는 집합을 그 집합에 속한 대표 원소로 나타냅니다. 즉, ‘집합 1’, ‘집합 3’, ‘집합 4’가 되는 것입니다.
이 예시에서 Union-Find 자료구조에서 할 수 있는 2가지 연산을 수행해 보겠습니다.
Find(x):x가 속한 집합을 알아내는 연산입니다.Find(2) = 1,Find(6) = 3,Find(4) = 4와 같이 그 집합의 대표 원소가 연산의 결과입니다.Union(x, y):x가 속한 집합과y가 속한 집합을 서로 합칩니다.Union(2, 3)을 하면{1, 2, 5}와{3, 6}이 합쳐져{1, 2, 3, 5, 6}이 됩니다.
Union-Find 자료구조는 다양한 방법으로 구현할 수 있습니다.
배열 구현
모든 원소가 자신이 속한 집합을 표에 적어 가지고 있는 방식으로 구현해 봅시다. 예를 들어, {1, 2, 5}, {3, 6}, {4, 7, 8}로 나누어진 원소들은 다음과 같은 배열로 나타내어집니다.
a[1~8] = {1, 1, 3, 4, 1, 3, 4, 4}
이 때 Union 연산과 Find 연산을 어떻게 구현할 수 있을지 생각해 봅시다.
Find(x):x가 속한 집합이 그대로 표에 적혀 있으므로 배열에서 값을 읽으면 됩니다.Union(x, y): 먼저x가 속한 집합과y가 속한 집합이 무엇인지 배열에서 값을 읽어 알아냅니다. 그리고,y가 속한 집합의 모든 원소들에 대해서, 배열에 있는 값을 교체해야 합니다. 예를 들어 위의 표에서Union(2, 3)을 하면 표에서 속한 집합이 ‘3’인 원소들(3, 6)의 값을 ‘1’로 바꿔야 합니다.
Find 연산은 배열에서 값을 읽는 것으로 상수 시간 O(1)에 간단히 수행할 수 있지만, Union 연산을 하려면 전체 표를 탐색해야 합니다. 따라서, Union 연산의 시간 복잡도는 원소 개수에 비례하는 O(N)입니다.
아래 소스 코드에서 Union-Find 자료구조를 배열로 구현하고 있습니다.
class UnionFind:
def __init__(self, N):
self.array = [0] * N
self.size = N
for i in range(N):
self.array[i] = i
def Find(self, x):
return self.array[x]
def Union(self, x, y):
xSet = self.array[x]
ySet = self.array[y]
for i in range(self.size):
if self.array[i] is ySet:
self.array[i] = xSet
연결 리스트 구현
다른 방법으로, 이번에는 연결 리스트를 통해 Union-Find 자료구조를 구현해 보겠습니다. 이 때, 각 원소들은 연결 리스트의 노드가 되고, 이 노드는 자신이 속한 집합의 다른 원소를 가리키고 있습니다. 아까의 예시 {1, 2, 5}, {3, 6}, {4, 7, 8}을 연결 리스트로 나타내면 다음과 같습니다.
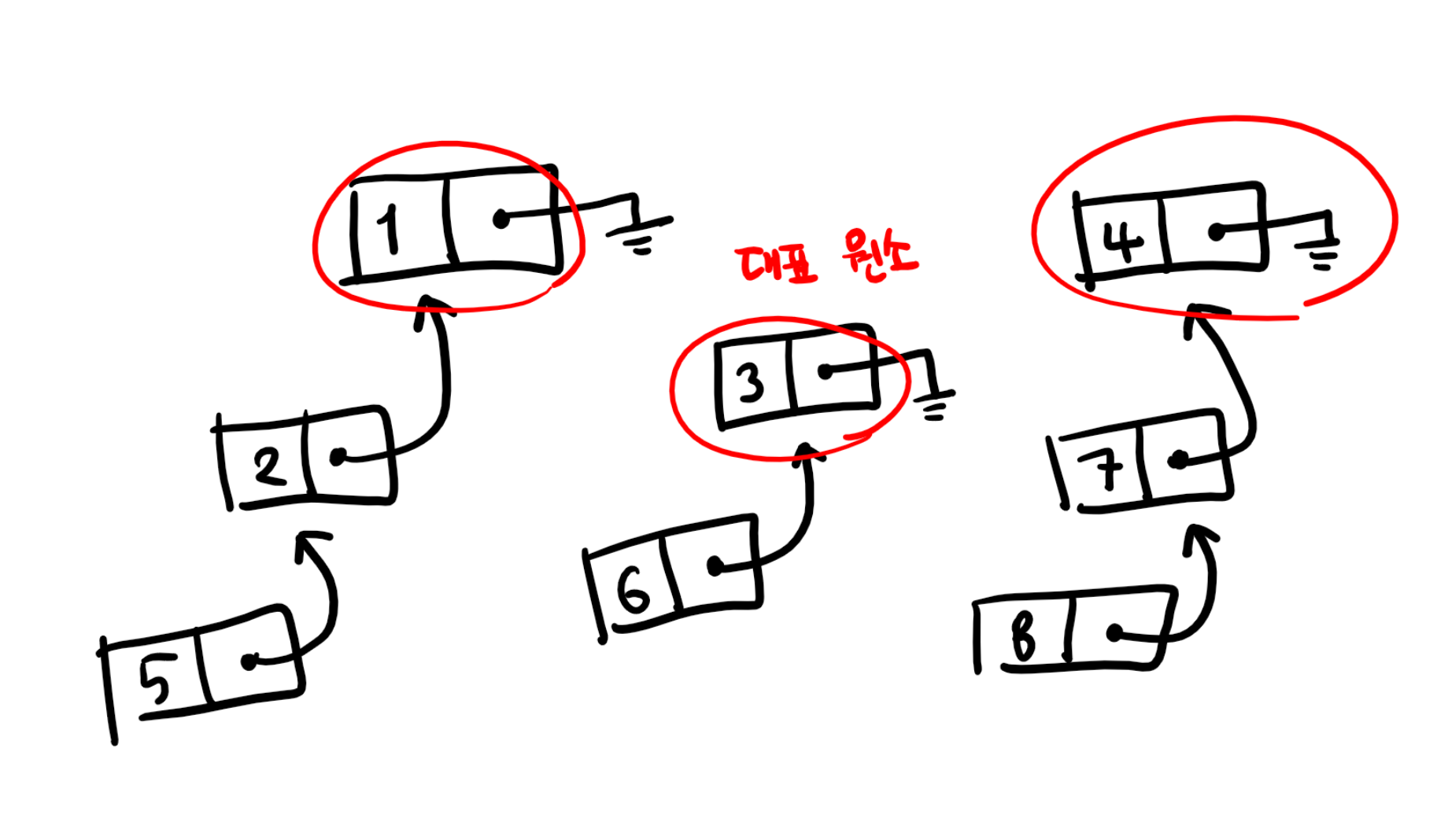
즉, 집합 하나를 연결 리스트 하나로 나타내고, 연결 리스트의 끝 원소가 집합의 대표 원소가 되는 방식입니다. 이러한 구조에서 Union 연산과 Find 연산을 구현하는 방법을 생각해 봅시다.
Find(x):x노드에서 출발하여, 계속해서 리스트를 따라가다가 만나는 끝 원소가 그 집합의 대표 원소가 됩니다. 예를 들어, 위의 예시에서Find(5)를 하면5->2->1을 따라가 1을 찾을 수 있습니다.Union(x, y): 먼저y노드에서 리스트의 끝 원소를 찾아서y가 속한 집합의 대표 원소를 알아냅니다. 그 다음,y집합 리스트의 끝 노드가x노드를 가리키도록 합니다. 예를 들어,Union(2, 3)을 하면 먼저 3부터 시작하여 끝 노드(3)를 찾고, 끝 노드가 2 노드를 가리키도록 합니다. 그림으로 그리면 다음과 같습니다.
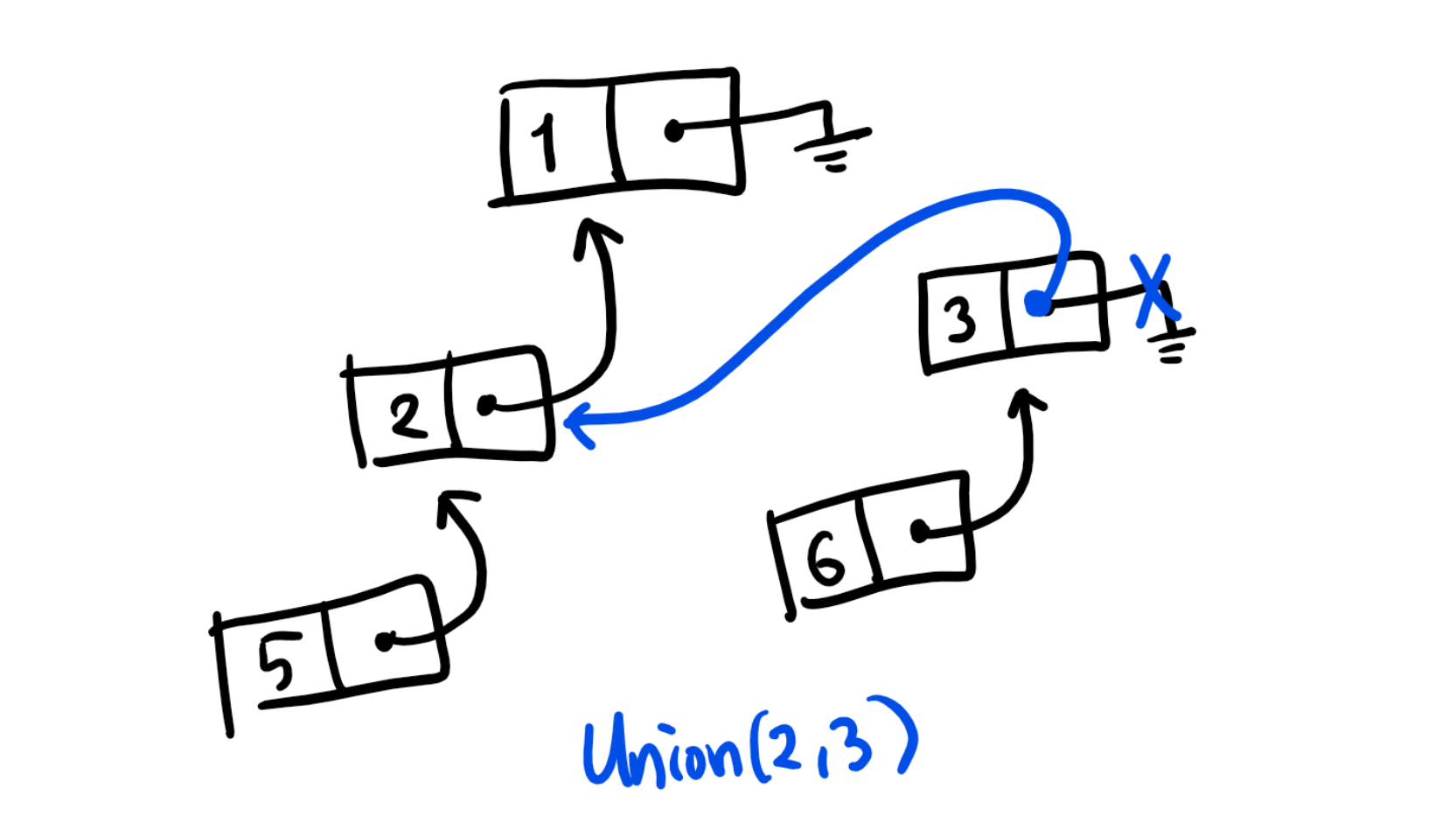
새롭게 만들어진 구조는 ‘가지’가 있어 연결 리스트와는 약간 다르지만, 어쨌든 Find(3), Find(6) 등의 연산을 수행하면 연결된 노드를 따라가 합쳐진 집합에서의 올바른 결과인 1을 얻을 수 있습니다.
연결 리스트를 활용한 구현에서는 Union과 Find 연산 모두 연결 리스트를 따라가면서 끝 노드를 찾아야 하기 때문에 원소의 총 개수에 비례하는 시간 복잡도가 소요됩니다.
아래 소스 코드는 연결 리스트를 활용한 Union-Find 자료구조의 구현입니다.
class Node:
def __init__(self, el):
self.next = None
self.el = el
class UnionFind:
def __init__(self, N):
self.array = map(lambda el: Node(el), range(N))
def Find(self, x):
cur = self.array[x]
while cur.next is not None:
cur = cur.next
return cur.el
def Union(self, x, y):
ySet = self.array[y]
while ySet.next is not None:
ySet = ySet.next
ySet.next = self.array[x]
압축을 통한 연결 리스트 최적화
연결 리스트를 이용한 Union-Find 자료구조의 구현은 각 연결 리스트의 길이가 늘어나면 비효율적으로 변합니다. Union과 Find 연산 모두 연결 리스트의 끝까지 탐색하는 것이 필요하기 때문입니다. 그렇다면, 연결 리스트의 길이를 줄여 Union과 Find 연산의 효율을 증가시키는 것은 어떨까요?
예를 들어, 집합을 나타낸 다음 두 개의 연결 리스트는 Union과 Find 연산 모두에게 똑같이 인식되지만, 두 연산을 수행하는 데 필요한 노드 탐색의 수는 큰 차이가 납니다.
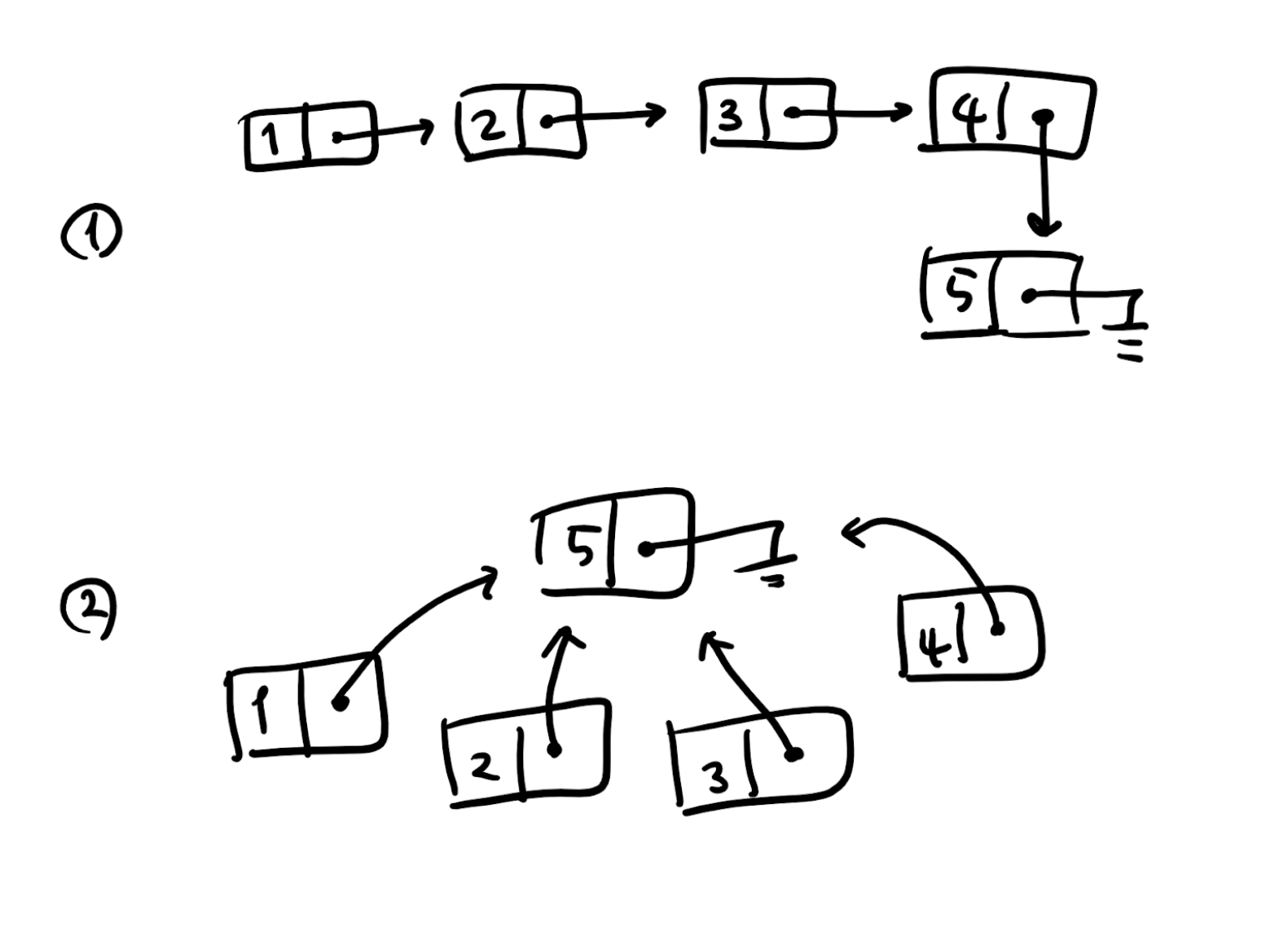
만약 우리가 적절한 처리를 통해 1번처럼 생긴 연결 리스트를 2번처럼 만들 수 있다면, Union, Find 연산이 빠르게 동작할 것입니다. 이를 위해, Find 연산을 수행할 때마다 1번처럼 노드가 여러 개 이어진 구조를 압축해서 2번과 같이 만들어 줍니다.
def Find(self, x):
cur = self.array[x]
while cur.next is not None:
cur = cur.next
end_node = cur
cur = self.array[x]
while cur.next is not None:
next = cur.next
cur.next = end_node
cur = next
return end_node.el
그리고, Union(x, y) 함수에서도 y가 속한 연결 리스트의 끝 노드를 찾을 때도 압축을 수행하기 위해 Find(y)로 찾아줍니다.
def Union(self, x, y):
ySet = self.Find(y)
self.array[ySet].next = self.array[x]
Weight를 통한 연결 리스트 최적화
연결 리스트의 길이를 줄일 수 있는 다른 방법으로는, Union(x, y)로 두 연결 리스트를 합칠 때 무조건 y의 끝 노드를 x 노드에 연결하는 것이 아니라, x와 y가 속한 연결 리스트의 길이 중 작은 리스트를 큰 리스트에 붙이면 반대로 할 때보다 합쳐진 리스트의 길이가 줄어들게 됩니다. 또, 붙일 때도 x 노드에 바로 붙이는 것이 아니라 x 노드가 속한 리스트의 끝에 붙여서 전체 길이를 줄어들게 해 줍니다.
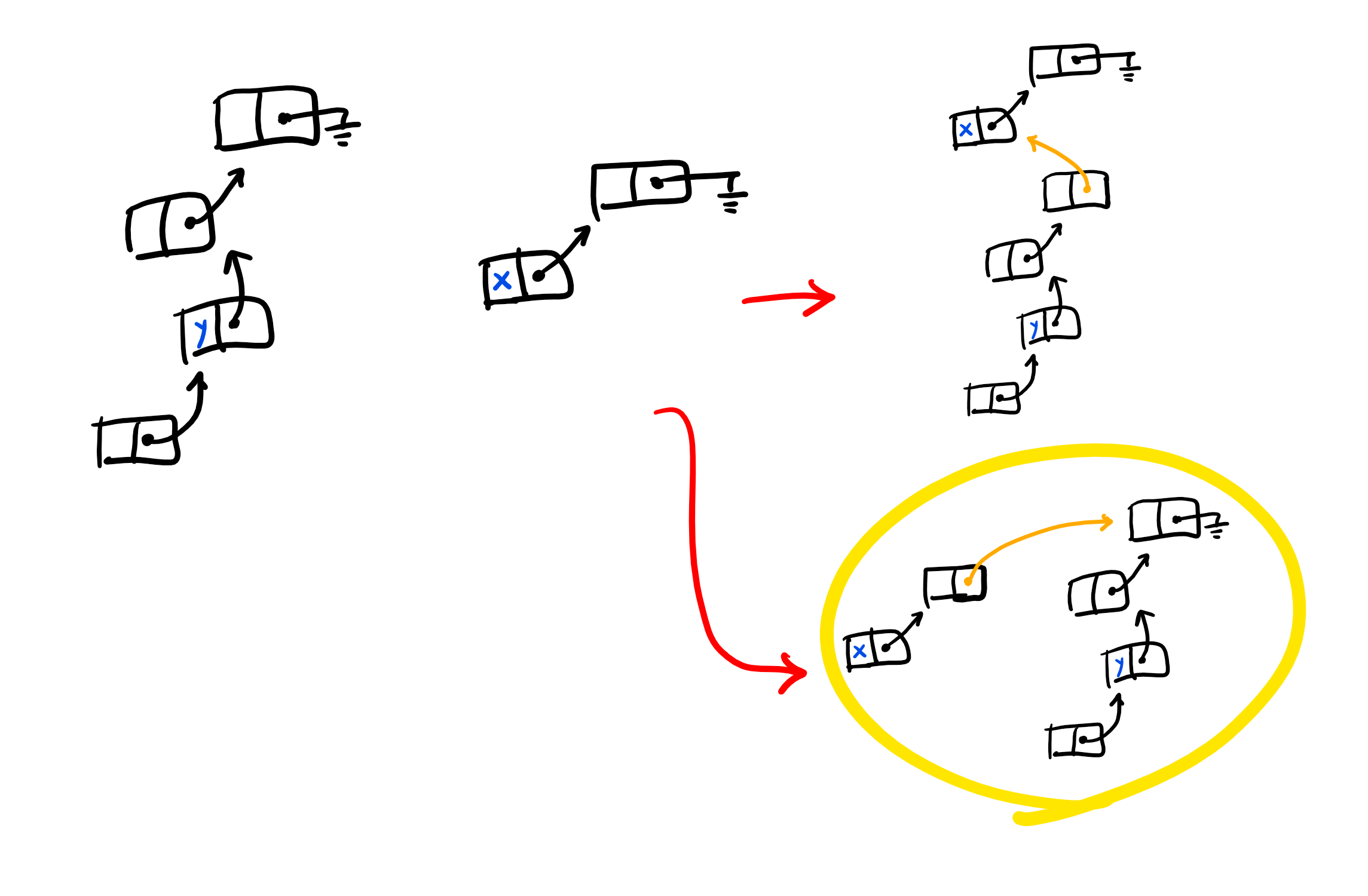
이를 위해, Union-Find 자료구조에서 각 노드가 몇 개의 노드를 아래에 달고 있는지 저장하면서 진행합니다. 이를 계산하는 것은, Union 연산을 할 때마다 합쳐 주기만 하면 되므로 매우 쉽습니다.
def __init__(self, N):
self.array = map(lambda el: Node(el), range(N))
self.weight = [1] * N
def Union(self, x, y):
xSet = self.Find(x)
ySet = self.Find(y)
if self.weight[xSet] < self.weight[ySet]:
self.array[xSet].next = self.array[ySet]
self.weight[ySet] += self.weight[xSet]
else
self.array[ySet].next = self.array[xSet]
self.weight[xSet] += self.weight[yset]
놀랍게도, 이 두 가지 처리만으로도 평균적인 연산의 시간 복잡도가 개선됩니다. 정확한 시간 복잡도는 수학적으로 복잡한 계산을 해야 하지만, 일반적인 경우에는 원소의 개수가 아주 많더라도 연결 리스트의 최대 길이가 4~5를 넘지 않습니다! 따라서, Union 연산과 Find 연산 모두 O(1)의 시간 복잡도에 동작한다고 가정해도 충분한 수준입니다.
이렇게 동일한 자료구조를 3가지 다른 방법으로 구현하며 자료구조가 수행하는 연산은 동일하지만, 연산의 구현 방법에 따라 시간 복잡도가 서로 달라지는 것을 경험해 볼 수 있었습니다. 문제 해결에 자료구조를 적용할 때는 자료구조에서 주로 수행해야 하는 연산이 무엇인지를 고려하여 그 연산에 유리한 자료구조와 구현 방법을 사용해야 하겠습니다.